Misschien gaat het met dat curriculumpuntgedoe net als met het lerarenregister... Een hoop gedoe maar uiteindelijk wordt het niks...
Ik wist niet dat er nog mensen waren die dat curriculumdinges nog serieus namen. Misschien een beter idee...!:-)
maandag 9 december 2019
zondag 8 december 2019
Kwadraatafsplitsen
\(
\begin{array}{l}
\left\{ \begin{array}{l}
L + W = 150 \\
L \cdot W = 4400 \\
\end{array} \right. \\
\left\{ \begin{array}{l}
L + W = 150 \\
L = \frac{{4400}}{W} \\
\end{array} \right. \\
\left\{ \begin{array}{l}
\frac{{4400}}{W} + W = 150 \\
L = \frac{{4400}}{W} \\
\end{array} \right. \\
\left\{ \begin{array}{l}
4400 + W^2 = 150W \\
L = \frac{{4400}}{W} \\
\end{array} \right. \\
\left\{ \begin{array}{l}
W^2 - 150W + 4400 = 0 \\
L = \frac{{4400}}{W} \\
\end{array} \right. \\
W^2 - 150W + 4400 = 0 \\
(W - 75)^2 - 5625 + 4400 = 0 \\
(W - 75)^2 - 1225 = 0 \\
(W - 75)^2 = 1225 \\
W - 75 = \pm 35 \\
W = 40 \vee W = 110 \\
\end{array}
\)
donderdag 21 november 2019
Vooruitgang
vrijdag 8 november 2019
Naschrift
\(
\eqalign{
& P_{eik} = pq^4 \cr
& P_{\neg eik} = (1 - p)(1 - q)^4 \cr
& P_R = \frac{{pq^4 }}
{{pq^4 + (1 - p)(1 - q)^4 }} \cr
& P_{q = \frac{1}
{2}} = \frac{{p\left( {\frac{1}
{2}} \right)^4 }}
{{p\left( {\frac{1}
{2}} \right)^4 + (1 - p)(1 - \left( {\frac{1}
{2}} \right))^4 }} \cr
& P_{q = \frac{1}
{2}} = \frac{p}
{{p + (1 - p)}} = p \cr}
\)
woensdag 6 november 2019
Naschrift
\(
\eqalign{
& f(x) = \ln \left( {4\left( {3x - x^2 } \right)^{ - 2} } \right) \cr
& f(x) = \ln (4) + \ln \left( {\left( {3x - x^2 } \right)^{ - 2} } \right) \cr
& f(x) = \ln (4) - 2\ln \left( {3x - x^2 } \right) \cr
& f'(x) = \frac{{ - 2}}
{{3x - x^2 }} \cdot \left( {3 - 2x} \right) \cr
& f'(x) = \frac{{ - 6 + 4x}}
{{3x - x^2 }} \cr
& f'(x) = \frac{{4x - 6}}
{{3x - x^2 }} \cr}
\)
donderdag 26 september 2019
Kleine aanvulling...:-)
\(
\eqalign{\frac{{\sqrt A }}
{{\sqrt B }} = \sqrt {\frac{A}
{B}} \,\,\,mits\,\,\,A \geqslant 0 \wedge B \gt 0}
\)
{{\sqrt B }} = \sqrt {\frac{A}
{B}} \,\,\,mits\,\,\,A \geqslant 0 \wedge B \gt 0}
\)
maandag 23 september 2019
Dat is een kwestie van het orde houden...
Dat ‘Dat is de kwestie van het orde houden…’ begrijp ik niet. Mijn ervaring is dat klassenmanagement (zeg maar orde!) veel belangrijker is dan vakinhoud. Na het klassemanagement komt de (vak-)didactiek, allerlei ongewenste moderniteiten en nog zo wat. Aan het eind van de tunnel komt de vakinhoud! Maar hoe moeilijk kan dat zijn? Die staat in het boek en anders kijk je maar op internet. Er zijn vast wel plekken waar je vragen kan stellen. Nee… zo moeilijk is het allemaal niet. Alhoewel…😑
Naschrift
Er zou sprake kunnen zijn van ironie. Sterker nog: ik weet het wel zeker. Het idee dat iedereen elk vak kan geven (zo gaat dat tegenwoordig) is daarmee (inderdaad) werkelijkheid geworden. Dat zoiets niet werkt lijkt me duidelijk. Dus ik bedoel maar… Dat wordt niks…:-)
Naschrift
Er zou sprake kunnen zijn van ironie. Sterker nog: ik weet het wel zeker. Het idee dat iedereen elk vak kan geven (zo gaat dat tegenwoordig) is daarmee (inderdaad) werkelijkheid geworden. Dat zoiets niet werkt lijkt me duidelijk. Dus ik bedoel maar… Dat wordt niks…:-)
maandag 24 juni 2019
Elektriciteitsverbruik
Ik had op elektriciteitsverbruik in eerste instantie gebruik gemaakt van integralen. Dat was vooral vanwege de oorspronkelijke titel 'integralen' en de gekozen categorie 'integreren'. Maar, zoals @GHvD opmerkte, zat er wel een addertje onder het gras. Met het verbruik per jaar zou je moeten rekenen met discrete waarden.
Daar zit wat in. Uiteindelijk ben ik er wel uitgekomen, geloof ik, maar wat nu precies de bedoeling was zullen we nooit weten...
Formule
\(
\eqalign{
& V_{gemiddeld} = \frac{{S_{20} }}
{{20}} = \frac{{3\root {10} \of 2 \cdot v_0 }}
{{20(\root {10} \of 2 - 1)}} \cr}
\)
Voorbeeld
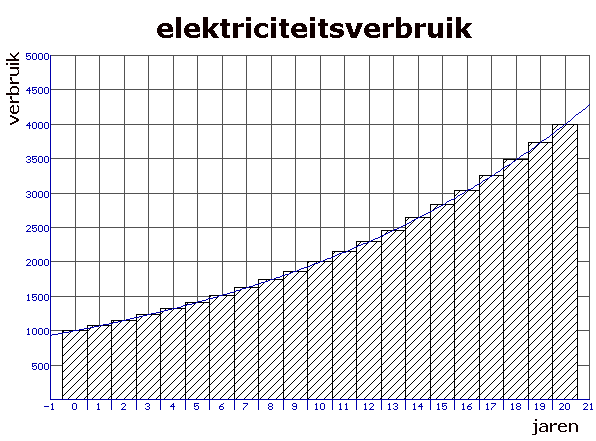
Neem \(v_0=1000\). In Excel krijg je dan zoiets als:
De formule hierboven geeft \(V_{gemiddeld}=2.239,9\) dus dat klopt...:-)
Hier kan je dan misschien toch nog wel iets doen met een integraal. Je moet wel even goed naar de grenzen kijken, maar dan heb je ook wat.
\(
\eqalign{V_{gemiddeld} = \frac{{\int\limits_{t = \frac{1}
{2}}^{20\frac{1}
{2}} {1000 \cdot e^{\frac{{\ln (2)}}
{{10}}t} dt} }}
{{20}} \approx 2240,4}
\)
Of, maar dan meer in het algemeen, voor een willekeurige waarde van \(v_0\):
\(
\eqalign{V_{gemiddeld} = v_0 \cdot \frac{{3 \cdot \root {20} \of 2 }}
{{2 \cdot \ln (2)}}}
\)
Ik bedoel maar. Ik vermaak me wel...:-)
Daar zit wat in. Uiteindelijk ben ik er wel uitgekomen, geloof ik, maar wat nu precies de bedoeling was zullen we nooit weten...
Formule
\(
\eqalign{
& V_{gemiddeld} = \frac{{S_{20} }}
{{20}} = \frac{{3\root {10} \of 2 \cdot v_0 }}
{{20(\root {10} \of 2 - 1)}} \cr}
\)
Voorbeeld
Neem \(v_0=1000\). In Excel krijg je dan zoiets als:
| jaar | verbruik |
| 1 | 1.072 |
| 2 | 1.149 |
| 3 | 1.231 |
| 4 | 1.320 |
| 5 | 1.414 |
| 6 | 1.516 |
| 7 | 1.625 |
| 8 | 1.741 |
| 9 | 1.866 |
| 10 | 2.000 |
| 11 | 2.144 |
| 12 | 2.297 |
| 13 | 2.462 |
| 14 | 2.639 |
| 15 | 2.828 |
| 16 | 3.031 |
| 17 | 3.249 |
| 18 | 3.482 |
| 19 | 3.732 |
| 20 | 4.000 |
| gemiddeld | 2.240 |
De formule hierboven geeft \(V_{gemiddeld}=2.239,9\) dus dat klopt...:-)

Hier kan je dan misschien toch nog wel iets doen met een integraal. Je moet wel even goed naar de grenzen kijken, maar dan heb je ook wat.
\(
\eqalign{V_{gemiddeld} = \frac{{\int\limits_{t = \frac{1}
{2}}^{20\frac{1}
{2}} {1000 \cdot e^{\frac{{\ln (2)}}
{{10}}t} dt} }}
{{20}} \approx 2240,4}
\)
Of, maar dan meer in het algemeen, voor een willekeurige waarde van \(v_0\):
\(
\eqalign{V_{gemiddeld} = v_0 \cdot \frac{{3 \cdot \root {20} \of 2 }}
{{2 \cdot \ln (2)}}}
\)
Ik bedoel maar. Ik vermaak me wel...:-)
zaterdag 15 juni 2019
donderdag 13 juni 2019
Precies:-)
One of the symptoms of an approaching nervous breakdown is the belief that one's work is terribly important.
Bertrand Russell
Bertrand Russell
vrijdag 7 juni 2019
Wat moet je er mee?
De formule \(a(n)=(n-1)(4n-3)\) geeft \(a(23)=1958\).
- Wat moet je er mee?:-)
donderdag 6 juni 2019
Ik ben er klaar mee...:-)
"After all is said and done, a lot more will be said than done."
Unknown
quotationspage.com/quotes/Unknown
#mijnHML

Unknown
quotationspage.com/quotes/Unknown
#mijnHML

donderdag 30 mei 2019
Dat moet kunnen...
\(
\eqalign{
& f(x) = ax^2 + bx + c \cr
& I. \cr
& A:f(m) = am^2 + bm + c \cr
& B:f(n) = an^2 + bn + c \cr
& rico_{AB} = \frac{{am^2 + bm + c - \left( {an^2 + bn + c} \right)}}
{{m - n}} \cr
& rico_{AB} = \frac{{am^2 + bm + c - an^2 - bn - c}}
{{m - n}} \cr
& rico_{AB} = \frac{{a(m^2 - n^2 ) + b(m - n)}}
{{m - n}} \cr
& rico_{AB} = a\left( {m + n} \right) + b \cr
& II. \cr
& f'(x) = 2ax + b \cr
& C:f'\left( {\frac{{m + n}}
{2}} \right) = 2a \cdot \frac{{m + n}}
{2} + b \cr
& C:f'\left( {\frac{{m + n}}
{2}} \right) = a\left( {m + n} \right) + b \cr}
\)
dinsdag 21 mei 2019
De som van de delers
De som van de som van de delers
\(\eqalign{
a(n) = \sum\limits_{k = 1}^n {\sigma (k)} = \sum\limits_{k = 1}^n {k \cdot \left\lfloor {\frac{n}
{k}} \right\rfloor }
}\)
1, 4, 8, 15, 21, 33, 41, 56, 69, 87, 99, 127, 141, ...
De som van de delers
\(
\sigma (n) = a(n) - a(n - 1)
\)
1, 3, 4, 7, 6, 12, 8, 15, ...
Excel
Function SomDelers(n)
Dim k, som
som = 0
For k = 1 To n
som = som + k * Fix(n \ k)
Next k
SomDelers = som
End Function
Function Sigma(n)
If n > 1 Then
Sigma = SomDelers(n) - SomDelers(n - 1)
Else
Sigma = 1
End If
End Function
| n | a(n) | s(n) |
| 1 | 1 | 1 |
| 2 | 4 | 3 |
| 3 | 8 | 4 |
| 4 | 15 | 7 |
| 5 | 21 | 6 |
| 6 | 33 | 12 |
| 7 | 41 | 8 |
| 8 | 56 | 15 |
| 9 | 69 | 13 |
| 10 | 87 | 18 |
| 11 | 99 | 12 |
| 12 | 127 | 28 |
| 13 | 141 | 14 |
| 14 | 165 | 24 |
| 15 | 189 | 24 |
| 16 | 220 | 31 |
| 17 | 238 | 18 |
| 18 | 277 | 39 |
| 19 | 297 | 20 |
| 20 | 339 | 42 |
WisFaq
Excel
vrijdag 17 mei 2019
VWO 4 wiskunde B
Gegeven de functie \(
f_p \left( x \right) = x^3 + \frac{3}
{4}px^2
\).
- Voor welke \(q\) heeft \(f_{-4}(x)=q\) géén/precies één/precies twee/precies 3 oplossingen?
- Voor welke \(p\) heeft \(f_p(x)\) precies twee toppen?
- De lijn \(k:y=24x+b\) raakt de grafiek van \(f_p\) in het punt met \(x_A=2\). Bereken \(p\) en \(b\).
- Stel een formule op van de kromme waarop alle toppen van de grafiek van \(f_p\) liggen.
zaterdag 4 mei 2019
Opgave 2
\(
\begin{array}{l}
\left\{ \begin{array}{l}
x^2 + xy = 20 \\
y^2 + xy = 30 \to x = \frac{{30 - y^2 }}{y} \\
\end{array} \right. \\
\downarrow \\
\left( {\frac{{30 - y^2 }}{y}} \right)^2 + \frac{{30 - y^2 }}{y} \cdot y = 20 \\
\frac{{30(30 - y^2 )}}{{y^2 }} = 20 \\
900 - 30y^2 = 20y^2 \\
50y^2 = 900 \\
y^2 = 45 \\
y = - 3\sqrt 2 \vee y = 3\sqrt 2 \\
\left\{ \begin{array}{l}
x = - 2\sqrt 2 \\
y = - 3\sqrt 2 \\
\end{array} \right. \vee \left\{ \begin{array}{l}
x = 2\sqrt 2 \\
y = 3\sqrt 2 \\
\end{array} \right. \\
xy = 12 \\
\end{array}
\)
maandag 29 april 2019
Re: Limiet bepalen
Naar aanleiding van Re: Limiet bepalen had ik nog een uitwerking bedacht:
\( \eqalign{ & \mathop {\lim }\limits_{x \to 0} \frac{{2x}} {{\root 3 \of {x + 27} - 3}} = \cr & \mathop {\lim }\limits_{x \to 0} \frac{{2x}} {{\root 3 \of {x + 27} - 3}} \cdot \frac{{\root 3 \of {\left( {x + 27} \right)^2 } + 3\root 3 \of {x + 27} + 9}} {{\root 3 \of {\left( {x + 27} \right)^2 } + 3\root 3 \of {x + 27} + 9}} = \cr & \mathop {\lim }\limits_{x \to 0} \frac{{2x \cdot \left( {\root 3 \of {\left( {x + 27} \right)^2 } + 3\root 3 \of {x + 27} + 9} \right)}} {{x + 27 - 27}} = \cr & \mathop {\lim }\limits_{x \to 0} \frac{{2x \cdot \left( {\root 3 \of {\left( {x + 27} \right)^2 } + 3\root 3 \of {x + 27} + 9} \right)}} {x} = \cr & \mathop {\lim }\limits_{x \to 0} 2 \cdot \left( {\root 3 \of {\left( {x + 27} \right)^2 } + 3\root 3 \of {x + 27} + 9} \right) = 2 \cdot \left( {9 + 9 + 9} \right) = 54 \cr} \)
Maar er zijn meer wegen die naar Rome leiden....:-)
\( \eqalign{ & \mathop {\lim }\limits_{x \to 0} \frac{{2x}} {{\root 3 \of {x + 27} - 3}} = \cr & \mathop {\lim }\limits_{x \to 0} \frac{{2x}} {{\root 3 \of {x + 27} - 3}} \cdot \frac{{\root 3 \of {\left( {x + 27} \right)^2 } + 3\root 3 \of {x + 27} + 9}} {{\root 3 \of {\left( {x + 27} \right)^2 } + 3\root 3 \of {x + 27} + 9}} = \cr & \mathop {\lim }\limits_{x \to 0} \frac{{2x \cdot \left( {\root 3 \of {\left( {x + 27} \right)^2 } + 3\root 3 \of {x + 27} + 9} \right)}} {{x + 27 - 27}} = \cr & \mathop {\lim }\limits_{x \to 0} \frac{{2x \cdot \left( {\root 3 \of {\left( {x + 27} \right)^2 } + 3\root 3 \of {x + 27} + 9} \right)}} {x} = \cr & \mathop {\lim }\limits_{x \to 0} 2 \cdot \left( {\root 3 \of {\left( {x + 27} \right)^2 } + 3\root 3 \of {x + 27} + 9} \right) = 2 \cdot \left( {9 + 9 + 9} \right) = 54 \cr} \)
Maar er zijn meer wegen die naar Rome leiden....:-)
Opgave 1
\(
\begin{array}{l}
\left\{ \begin{array}{l}
a + b = 2ab \\
b + c = 3bc \\
a + c = 7ac \\
\end{array} \right. \\
\left\{ \begin{array}{l}
\frac{1}{b} + \frac{1}{a} = 2 \\
\frac{1}{c} + \frac{1}{b} = 3 \\
\frac{1}{c} + \frac{1}{a} = 7 \\
\end{array} \right. \\
\left\{ \begin{array}{l}
\frac{1}{b} + \frac{1}{a} = 2 \\
\frac{1}{c} - \frac{1}{a} = 1 \\
\frac{1}{c} + \frac{1}{a} = 7 \\
\end{array} \right. \\
\left\{ \begin{array}{l}
\frac{1}{b} + \frac{1}{a} = 2 \\
\frac{1}{c} - \frac{1}{a} = 1 \\
\frac{2}{c} = 8 \\
\end{array} \right. \\
\left\{ \begin{array}{l}
\frac{1}{b} + \frac{1}{a} = 2 \\
\frac{1}{c} - \frac{1}{a} = 1 \\
c = \frac{1}{4} \\
\end{array} \right. \\
\left\{ \begin{array}{l}
\frac{1}{b} + \frac{1}{a} = 2 \\
4 - \frac{1}{a} = 1 \\
c = \frac{1}{4} \\
\end{array} \right. \\
\left\{ \begin{array}{l}
\frac{1}{b} + \frac{1}{a} = 2 \\
a = \frac{1}{3} \\
c = \frac{1}{4} \\
\end{array} \right. \\
\left\{ \begin{array}{l}
\frac{1}{b} + 3 = 2 \\
a = \frac{1}{3} \\
c = \frac{1}{4} \\
\end{array} \right. \\
\left\{ \begin{array}{l}
b = - 1 \\
a = \frac{1}{3} \\
c = \frac{1}{4} \\
\end{array} \right. \\
\end{array}
\)
zaterdag 27 april 2019
zondag 14 april 2019
wizPROF 2018 - Vraag 7
Els en Fiona knippen beiden een rechthoekig velletje papier in tweeën. Els krijgt twee rechthoeken, elk met een omtrek van 40 cm. Fiona krijgt ook twee rechthoeken, maar dan elk met een omtrek van 50 cm. Toch hebben beiden eenzelfde velletje doorgeknipt.

\( \begin{array}{l} \left\{ \begin{array}{l} 2a + b = 40 \\ a + 2b = 50 \\ \end{array} \right. \\ \left\{ \begin{array}{l} 2a + b = 40 \\ 2a + 4b = 100 \\ \end{array} \right. \\ \left\{ \begin{array}{l} 3b = 60 \\ 2a + b = 40 \\ \end{array} \right. \\ \left\{ \begin{array}{l} b = 20 \\ a = 10 \\ \end{array} \right. \\ \end{array} \)
- Wat is de omtrek van het velletje papier waarmee ze begonnen?
A. 40 cm B. 50 cm C. 60 cm D. 80 cm E. 90 cm

\( \begin{array}{l} \left\{ \begin{array}{l} 2a + b = 40 \\ a + 2b = 50 \\ \end{array} \right. \\ \left\{ \begin{array}{l} 2a + b = 40 \\ 2a + 4b = 100 \\ \end{array} \right. \\ \left\{ \begin{array}{l} 3b = 60 \\ 2a + b = 40 \\ \end{array} \right. \\ \left\{ \begin{array}{l} b = 20 \\ a = 10 \\ \end{array} \right. \\ \end{array} \)
woensdag 3 april 2019
Een kwadratische vergelijking met breuken oplossen
\(
\eqalign{
& \frac{1}
{4}\left( {x + 1} \right)(x + 5) = - \frac{3}
{4} \cr
& \left( {x + 1} \right)(x + 5) = - 3 \cr
& x^2 + 6x + 5 = - 3 \cr
& x^2 + 6x + 8 = 0 \cr
& (x + 2)(x + 4) = 0 \cr
& x = - 2 \vee x = - 4 \cr}
\)
\eqalign{
& \frac{1}
{4}\left( {x + 1} \right)(x + 5) = - \frac{3}
{4} \cr
& \left( {x + 1} \right)(x + 5) = - 3 \cr
& x^2 + 6x + 5 = - 3 \cr
& x^2 + 6x + 8 = 0 \cr
& (x + 2)(x + 4) = 0 \cr
& x = - 2 \vee x = - 4 \cr}
\)
Het oplossen van een vergelijking
Op WisFaq staat een oplossing van een vergelijking met machten. In het antwoordmodel wordt er gekozen om te delen door 4x. Dat kan natuurlijk prima, maar eigenlijk vind ik dat niet handig en 't is een gemiste kans om nog 's wat kennis rondom machten te herhalen. Ik zou het liever zo doen:
\(
\eqalign{
& 2 \cdot 4^x - 4 \cdot 8^x = 0 \cr
& 2 \cdot 4^x = 4 \cdot 8^x \cr
& 4^x = 2 \cdot 8^x \cr
& \left( {2^2 } \right)^x = 2^1 \cdot \left( {2^3 } \right)^x \cr
& 2^{2x} = 2^1 \cdot 2^{3x} \cr
& 2^{2x} = 2^{3x + 1} \cr
& 2x = 3x + 1 \cr
& x = - 1 \cr}
\)
Maar waarom?
\(
\eqalign{
& 2 \cdot 4^x - 4 \cdot 8^x = 0 \cr
& 2 \cdot 4^x = 4 \cdot 8^x \cr
& 4^x = 2 \cdot 8^x \cr
& \left( {2^2 } \right)^x = 2^1 \cdot \left( {2^3 } \right)^x \cr
& 2^{2x} = 2^1 \cdot 2^{3x} \cr
& 2^{2x} = 2^{3x + 1} \cr
& 2x = 3x + 1 \cr
& x = - 1 \cr}
\)
Maar waarom?
- Het gaat hier om machten van 2. Als het lukt om beide leden te schrijven als 2A=2B en dus A=B ben je er. Dat is het doel en bij vergelijkingen met machten is dat een goede aanpak. Die paragraaf in het boek over het schrijven als één macht was dan niet voor niets geweest.
dinsdag 19 maart 2019
Los op
Los exact op:
\(
\eqalign{
& \left( {x^2 - x - 2} \right)^2 - x^3 = 10 \cr
& \left( {x^2 - x - 2} \right)\left( {x^2 - x - 2} \right) - x^3 = 10 \cr
& x^4 - x^3 - 2x^2 - x^3 + x^2 + 2x - 2x^2 + 2x + 4 - x^3 = 10 \cr
& x^4 - 3x^3 - 3x^2 + 4x - 6 = 0 \cr
& \left( {x^2 - x + 1} \right)\left( {x^2 - 2x - 6} \right) = 0 \cr
& x^2 - x + 1 = 0 \vee x^2 - 2x - 6 = 0 \cr
& x = 1 - \sqrt 7 \vee x = 1 + \sqrt 7 \cr}
\)
- \(
\left( {x^2 - x - 2} \right)^2 - x^3 = 10
\)
\(
\eqalign{
& \left( {x^2 - x - 2} \right)^2 - x^3 = 10 \cr
& \left( {x^2 - x - 2} \right)\left( {x^2 - x - 2} \right) - x^3 = 10 \cr
& x^4 - x^3 - 2x^2 - x^3 + x^2 + 2x - 2x^2 + 2x + 4 - x^3 = 10 \cr
& x^4 - 3x^3 - 3x^2 + 4x - 6 = 0 \cr
& \left( {x^2 - x + 1} \right)\left( {x^2 - 2x - 6} \right) = 0 \cr
& x^2 - x + 1 = 0 \vee x^2 - 2x - 6 = 0 \cr
& x = 1 - \sqrt 7 \vee x = 1 + \sqrt 7 \cr}
\)
zondag 17 maart 2019
Benadering voor de sinus
| x | sinus | benadering | verschil |
| 0.000000 | 0.000000 | 0.000000 | 0.000 |
| 0.130900 | 0.130526 | 0.131994 | 0.001 |
| 0.261799 | 0.258819 | 0.260355 | 0.002 |
| 0.392699 | 0.382683 | 0.383562 | 0.001 |
| 0.523599 | 0.500000 | 0.500000 | 0.000 |
| 0.654498 | 0.608761 | 0.608000 | 0.001 |
| 0.785398 | 0.707107 | 0.705882 | 0.001 |
| 0.916298 | 0.793353 | 0.792013 | 0.001 |
| 1.047198 | 0.866025 | 0.864865 | 0.001 |
| 1.178097 | 0.923880 | 0.923077 | 0.001 |
| 1.308997 | 0.965926 | 0.965517 | 0.000 |
| 1.439897 | 0.991445 | 0.991334 | 0.000 |
| 1.570796 | 1.000000 | 1.000000 | 0.000 |
| 1.701696 | 0.991445 | 0.991334 | 0.000 |
| 1.832596 | 0.965926 | 0.965517 | 0.000 |
| 1.963495 | 0.923880 | 0.923077 | 0.001 |
| 2.094395 | 0.866025 | 0.864865 | 0.001 |
| 2.225295 | 0.793353 | 0.792013 | 0.001 |
| 2.356194 | 0.707107 | 0.705882 | 0.001 |
| 2.487094 | 0.608761 | 0.608000 | 0.001 |
| 2.617994 | 0.500000 | 0.500000 | 0.000 |
| 2.748894 | 0.382683 | 0.383562 | 0.001 |
| 2.879793 | 0.258819 | 0.260355 | 0.002 |
| 3.010693 | 0.130526 | 0.131994 | 0.001 |
| 3.141593 | 0.000000 | 0.000000 | 0.000 |
| gemiddeld= | 0.001 |
woensdag 13 maart 2019
Omtrek en oppervlakte van een rechthoekige driehoek
Bereken exact de oppervlakte van de rechthoekige driehoek waarvan de omtrek 12 is en de ene rechthoekszijde 1 groter is dan de andere rechthoekszijde?
Uitwerking
\( \eqalign{ & x + x + 1 + \sqrt {x^2 + (x + 1)^2 } = 12 \cr & \sqrt {x^2 + (x + 1)^2 } = - 2x + 11 \cr & x^2 + x^2 + 2x + 1 = \left( { - 2x + 11} \right)^2 \cr & 2x^2 + 2x + 1 = 4x^2 - 44x + 121 \cr & 2x^2 - 46x + 120 = 0 \cr & x^2 - 23x + 60 = 0 \cr & (x - 3)(x - 20) = 0 \cr & x = 3 \vee x = 20\,\,\,(v.n.) \cr & x = 3 \cr} \)
De oppervlakte is 6.
Maar als de omtrek nu 's 10 is?
Je krijgt dan zoiets:
\(
\eqalign{
& x + x + 1 + \sqrt {x^2 + (x + 1)^2 } = 10 \cr
& \sqrt {x^2 + (x + 1)^2 } = - 2x + 9 \cr
& x^2 + (x + 1)^2 = ( - 2x + 9)^2 \cr
& x^2 + x^2 + 2x + 1 = 4x^2 - 36x + 81 \cr
& 2x^2 - 38x + 80 = 0 \cr
& x^2 - 19x + 40 = 0 \cr
& x = 9\frac{1}
{2} - \frac{1}
{2}\sqrt {201} \vee x = 9\frac{1}
{2} + \frac{1}
{2}\sqrt {201} \,\,\,(v.n.) \cr
& x = 9\frac{1}
{2} - \frac{1}
{2}\sqrt {201} \cr}
\)
De oppervlakte is 75-5√210
Uitwerking
\( \eqalign{ & x + x + 1 + \sqrt {x^2 + (x + 1)^2 } = 12 \cr & \sqrt {x^2 + (x + 1)^2 } = - 2x + 11 \cr & x^2 + x^2 + 2x + 1 = \left( { - 2x + 11} \right)^2 \cr & 2x^2 + 2x + 1 = 4x^2 - 44x + 121 \cr & 2x^2 - 46x + 120 = 0 \cr & x^2 - 23x + 60 = 0 \cr & (x - 3)(x - 20) = 0 \cr & x = 3 \vee x = 20\,\,\,(v.n.) \cr & x = 3 \cr} \)
De oppervlakte is 6.
Maar als de omtrek nu 's 10 is?
Je krijgt dan zoiets:
\(
\eqalign{
& x + x + 1 + \sqrt {x^2 + (x + 1)^2 } = 10 \cr
& \sqrt {x^2 + (x + 1)^2 } = - 2x + 9 \cr
& x^2 + (x + 1)^2 = ( - 2x + 9)^2 \cr
& x^2 + x^2 + 2x + 1 = 4x^2 - 36x + 81 \cr
& 2x^2 - 38x + 80 = 0 \cr
& x^2 - 19x + 40 = 0 \cr
& x = 9\frac{1}
{2} - \frac{1}
{2}\sqrt {201} \vee x = 9\frac{1}
{2} + \frac{1}
{2}\sqrt {201} \,\,\,(v.n.) \cr
& x = 9\frac{1}
{2} - \frac{1}
{2}\sqrt {201} \cr}
\)
De oppervlakte is 75-5√210
zondag 10 maart 2019
Dat kan ook...:-)
Op Differentiëren van goniometrische functies met de kettingregel krijg je er wel een antwoord uit.
Mijn Derive geeft:
\( f'(x) = 25\sin^3 (2x)\sin (4x) \)
Dat kan ook, maar hoe kom je er aan?
\(
\eqalign{
& f(x) = 5 \cdot \sin ^5 (2x) \cr
& f'(x) = 5 \cdot 5 \cdot \sin ^4 (2x) \cdot \cos (2x) \cdot 2 \cr
& f'(x) = 50\sin ^4 (2x)\cos (2x) \cr}
\)
Met \(
\sin (2A) = 2\sin (A)\cos (A)
\) krijg je:
\(
\eqalign{
& f'(x) = 50\sin ^4 (2x)\cos (2x) \cr
& f'(x) = 50\sin ^3 (2x)\sin (2x)\cos (2x) \cr
& f'(x) = 50\sin ^3 (2x)\frac{1}
{2}\sin (4x) \cr
& f'(x) = 25\sin^3 (2x)\sin (4x) \cr}
\)
De vraag is alleen nog waarom je dat zou willen, maar kennelijk zit in het programma ingebakken om de exponenten zo klein mogelijk te houden. Dat is een mooi streven...:-)
Mijn Derive geeft:
\( f'(x) = 25\sin^3 (2x)\sin (4x) \)
Dat kan ook, maar hoe kom je er aan?
\(
\eqalign{
& f(x) = 5 \cdot \sin ^5 (2x) \cr
& f'(x) = 5 \cdot 5 \cdot \sin ^4 (2x) \cdot \cos (2x) \cdot 2 \cr
& f'(x) = 50\sin ^4 (2x)\cos (2x) \cr}
\)
Met \(
\sin (2A) = 2\sin (A)\cos (A)
\) krijg je:
\(
\eqalign{
& f'(x) = 50\sin ^4 (2x)\cos (2x) \cr
& f'(x) = 50\sin ^3 (2x)\sin (2x)\cos (2x) \cr
& f'(x) = 50\sin ^3 (2x)\frac{1}
{2}\sin (4x) \cr
& f'(x) = 25\sin^3 (2x)\sin (4x) \cr}
\)
De vraag is alleen nog waarom je dat zou willen, maar kennelijk zit in het programma ingebakken om de exponenten zo klein mogelijk te houden. Dat is een mooi streven...:-)
zaterdag 9 maart 2019
vrijdag 8 maart 2019
zaterdag 2 maart 2019
Begeleidingsuren
Het 'systeem' van begeleidingsuren werkt niet. Het is kennelijk niet
echt mogelijk de juiste leerlingen in de juiste setting met de juiste
houding te kunnen bedienen. In dat geval kan je er maar beter mee
stoppen... #mijnHML dus bij deze...
vrijdag 22 februari 2019
dinsdag 19 februari 2019
Rijtjes...
Geef de volgende term:
- 1, 2, 4, 8, 16, ...
- 1, 1, 2, 3, 5, 8, 13, 21, ...
- 1, 9, 2, 8, 3, 7, 4, 6, 5, ...
- 1, 11, 121, 1331, 14641, ...
- 1, 121, 12321, 1234321, 123454321, 12345654321, 1234567654321, 123456787654321, 12345678987654321, ...
- 1, 10, 11, 100, 101, 110, ...
- o, t, t, f, f, s, s, e, n, t, e, t, t, f, f, s, s, e, n, t, t, t, t, t, ...
- 0, 5, 8, 12, 20, 50, ...
- 30, 105, 385, 1001, 2431, ...
- 1, 11, 21, 1211, 111221, 312211, ...
zaterdag 9 februari 2019
woensdag 6 februari 2019
Rekentoets
"Middelbare scholieren krijgen vanaf komend schooljaar geen aparte rekentoets meer. De huidige landelijke toets verdwijnt definitief en rekenen wordt weer een onderdeel van wiskunde en andere vakken."
bron
bron
Abonneren op:
Reacties (Atom)