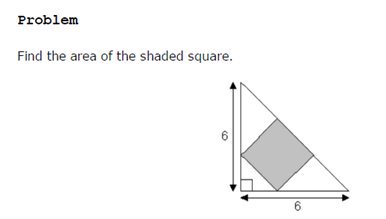
maandag 30 juli 2018
zaterdag 28 juli 2018
Nikolay Bogdanov-Belsky
In 1895, Nikolay Bogdanov-Belsky painted the famous: "Mental Arithmetic.
In the Public School of S. Rachinsky." The problem on the blackboard is
(10²+11²+12²+13²+14²)/365, can you find a way to solve it with mental
arithmetic?
\( \eqalign{ & \frac{{10^2 + 11^2 + 12^2 + 13^2 + 14^2 }} {{365}} = \cr & \frac{{10^2 + \left( {10 + 1} \right)^2 + (10 + 2)^2 + (10 + 3)^2 + (10 + 4)^2 }} {{365}} = \cr & \frac{{5 \cdot 10^2 + 2 \cdot 10 + 4 \cdot 10 + 6 \cdot 10 + 8 \cdot 10 + 1 + 4 + 9 + 16}} {{365}} = \cr & \frac{{500 + 200 + 30}} {{365}} = \cr & \frac{{730}} {{365}} = 2 \cr} \)
\( \eqalign{ & \frac{{10^2 + 11^2 + 12^2 + 13^2 + 14^2 }} {{365}} = \cr & \frac{{10^2 + \left( {10 + 1} \right)^2 + (10 + 2)^2 + (10 + 3)^2 + (10 + 4)^2 }} {{365}} = \cr & \frac{{5 \cdot 10^2 + 2 \cdot 10 + 4 \cdot 10 + 6 \cdot 10 + 8 \cdot 10 + 1 + 4 + 9 + 16}} {{365}} = \cr & \frac{{500 + 200 + 30}} {{365}} = \cr & \frac{{730}} {{365}} = 2 \cr} \)
woensdag 18 juli 2018
Week 34
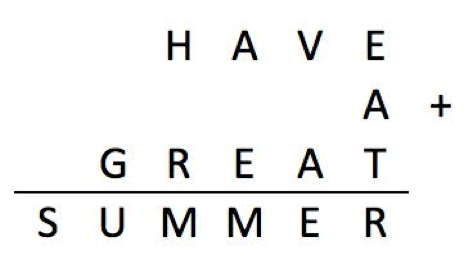
This is the end...
Met ingang van 18-7-2018 stop ik definitief met de weekpuzzels. 't Was leuk maar de koek is op...:-)
zondag 15 juli 2018
Week 32
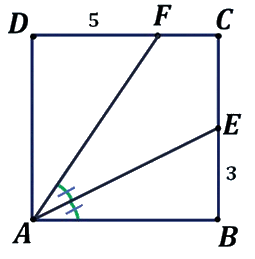
ABCD is een vierkant met AE de deellijn van de hoek BAF.
- Bereken de lengte van AF.
Abonneren op:
Posts (Atom)