Goniometrische functie

Stel een passend functievoorschrift op (2)

 Uit HAVO wiskunde B hoofdstuk 14:

Dat is een mooi idee. De vraag wordt geleid en leidt uiteindelijk tot:

Dat is (op zich) prima, maar in het licht van de gekozen didactiek ligt de formule voor de sinus niet helemaal voor de hand. Als je voor c de waarde kiest waar bij de grafiek stijgend door de evenwichtsstand gaat dan zou ik geneigd zijn het punt \((1\frac{3}{4}\pi,0)\) te nemen:

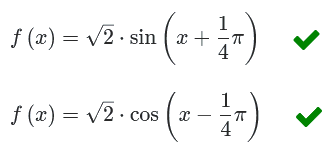
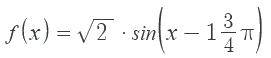
De vraag is nu: zou het programma dat goed vinden?👅

HAVO wiskunde B hoofdstuk 14 - Test jezetf 4

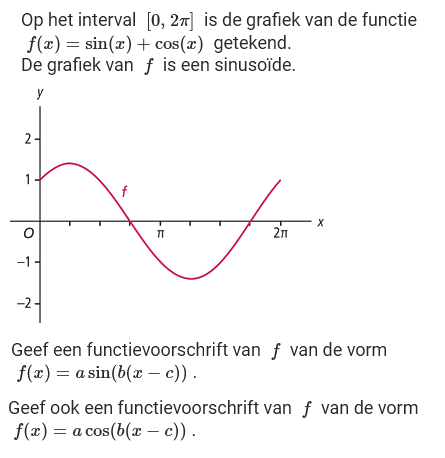
Stel een passend functievoorschrift op

Uit HAVO wiskunde B hoofdstuk 14:

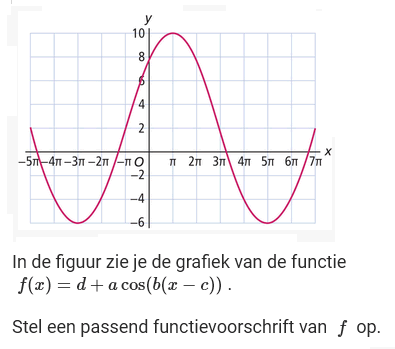
Het gaat hier om cosinus dus voor de waarde van c zoek je een top met een maximum. Het punt \((\pi,10)\) ligt voor de hand. Waarschijnlijk zal het antwoord geen problemen geven:

Maar bij de tweede opgave moet je toch even opletten...

Normale mensen zullen waarschijnlijk kiezen voor de sinus. Je krijgt dan:

Dat is natuurlijk prima. Je hebt een punt waarbij de grafiek stijgend door de evenwichtsstand gaat dus neem de sinus met c=4. Maar je kunt ook de cosinus nemen:

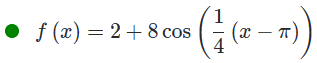
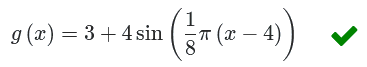
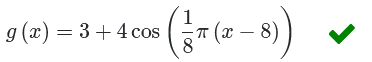
Dat kan ook... maar dat antwoord moet je er dan wel apart inzetten. Het programma zou het in eerste instantie niet goed rekenen.

HAVO B hoofdstuk 14 - Extra oefening E1

Twee gelijkbenige driehoeken

Naar aanleiding van Twee gelijkbenige driehoeken. 't Is dan wel niet echt handig, maar 't kan wel...

\( \eqalign{ & \frac{{BC}} {{\sin 20^\circ }} = \frac{{AC}} {{\sin 80^\circ }} \Rightarrow BC = \frac{{AC \cdot \sin 20^\circ }} {{\sin 80^\circ }} \cr & \frac{{CD}} {{\sin 40^\circ }} = \frac{{AC}} {{\sin 100^\circ }} \Rightarrow CD = \frac{{AC \cdot \sin 40^\circ }} {{\sin 100^\circ }} \cr & BC + CD = \frac{{AC \cdot \sin 20^\circ }} {{\sin 80^\circ }} + \frac{{AC \cdot \sin 40^\circ }} {{\sin 100^\circ }} \cr & BC + CD = \frac{{AC \cdot \sin 20^\circ }} {{\sin 80^\circ }} + \frac{{AC \cdot \sin 40^\circ }} {{\sin 80^\circ }} \cr & BC + CD = \frac{{AC \cdot \sin 20^\circ + AC \cdot \sin 40^\circ }} {{\sin 80^\circ }} \cr & BC + CD = \frac{{AC \cdot \left( {\sin 20^\circ + \sin 40^\circ } \right)}} {{\sin 80^\circ }} \cr & BC + CD = \frac{{AC \cdot \left( {2\sin \frac{{20^\circ + 40^\circ }} {2}\cos \frac{{20^\circ - 40^\circ }} {2}} \right)}} {{\sin 80^\circ }} \cr & BC + CD = \frac{{AC \cdot \left( {2\sin 30^\circ \cos 10^\circ } \right)}} {{\sin 80^\circ }} \cr & BC + CD = \frac{{AC \cdot \cos 10^\circ }} {{\sin 80^\circ }} = AC \cr } \)

Omdat het kan...:-)

Dat kan ook...:-)

Op Differentiëren van goniometrische functies met de kettingregel krijg je er wel een antwoord uit.

Mijn Derive geeft:

 \( f'(x) = 25\sin^3 (2x)\sin (4x) \)

Dat kan ook, maar hoe kom je er aan?

\(
\eqalign{
  & f(x) = 5 \cdot \sin ^5 (2x)  \cr
  & f'(x) = 5 \cdot 5 \cdot \sin ^4 (2x) \cdot \cos (2x) \cdot 2  \cr
  & f'(x) = 50\sin ^4 (2x)\cos (2x) \cr}
\)

Met \(
\sin (2A) = 2\sin (A)\cos (A)
\) krijg je:

\(
\eqalign{
  & f'(x) = 50\sin ^4 (2x)\cos (2x)  \cr
  & f'(x) = 50\sin ^3 (2x)\sin (2x)\cos (2x)  \cr
  & f'(x) = 50\sin ^3 (2x)\frac{1}
{2}\sin (4x)  \cr
  & f'(x) = 25\sin^3 (2x)\sin (4x) \cr}
\)

De vraag is alleen nog waarom je dat zou willen, maar kennelijk zit in het programma ingebakken om de exponenten zo klein mogelijk te houden. Dat is een mooi streven...:-)

Proof en pudding

\( \eqalign{ & \frac{{\cos \left( u \right) + \sin \left( u \right)}} {{\cos \left( u \right) - \sin \left( u \right)}} = \frac{{1 + \sin (2u)}} {{\cos (2u)}} \cr & \frac{{\left( {\cos \left( u \right) + \sin \left( u \right)} \right)\left( {\cos \left( u \right) - \sin \left( u \right)} \right)}} {{\left( {\cos \left( u \right) - \sin \left( u \right)} \right)^2 }} = \frac{{1 + \sin (2u)}} {{\cos (2u)}} \cr & \frac{{\cos ^2 \left( u \right) - \sin ^2 \left( u \right)}} {{\cos ^2 (u) - 2\sin (u)\cos (u) + \sin ^2 (u)}} = \frac{{1 + \sin (2u)}} {{\cos (2u)}} \cr & \frac{{\cos \left( {2u} \right)}} {{1 - \sin (2u)}} = \frac{{1 + \sin (2u)}} {{\cos (2u)}} \cr & \cos ^2 (2u) = 1 - \sin ^2 (2u) \cr & \sin ^2 (2u) + \cos ^2 (2u) = 1 \cr & {\text{Klopt!}} \cr} \)