\(
\eqalign{
& \int {{{\tan (\ln (\sqrt x ))} \over x}} \,dx = \cr
& \int {\tan \left( {{1 \over 2}\ln (x)} \right)} \cdot {1 \over x}\,dx = \cr
& \int {\tan \left( {{1 \over 2}\ln (x)} \right)} \,d\left( {\ln (x)} \right) = \cr
& \downarrow u = \ln (x) \cr
& \int {\tan \left( {{1 \over 2}u} \right)} \,du = \cr
& \int {{{\sin \left( {{1 \over 2}u} \right)} \over {\cos \left( {{1 \over 2}u} \right)}}} \,du = \cr
& \int {{{ - 2} \over {\cos \left( {{1 \over 2}u} \right)}}}
\cdot - {1 \over 2}\sin \left( {{1 \over 2}u} \right)\,du = \cr
& \int {{{ - 2} \over {\cos \left( {{1 \over 2}u} \right)}}} \cdot
\,d\left( {\cos \left( {{1 \over 2}u} \right)} \right) = \cr
& \downarrow v = \cos \left( {{1 \over 2}u} \right) \cr
& \int {{{ - 2} \over v}} \cdot \,dv = \cr
& - 2\ln (v) + C = \cr
& - 2\ln \left( {\cos \left( {{1 \over 2}u} \right)} \right) + C = \cr
& - 2\ln \left( {\cos \left( {{1 \over 2}\ln (x)} \right)} \right) + C \cr
& - 2\ln \left( {\cos \left( {\ln (\sqrt x )} \right)} \right) + C \cr}
\)
Posts tonen met het label wiskundeD. Alle posts tonen
Posts tonen met het label wiskundeD. Alle posts tonen
woensdag 3 juni 2020
maandag 30 maart 2020
Transformaties
Gegeven:
\( \eqalign{ & f(x) = x^2 \cr & g(x) = x^2 - 4x + 3 \cr} \)
De gemeenschappelijke raaklijn raakt \(f\) in \(x=p\) en \(g\) in \(x=q\).
Je kunt \(g\) opvatten als een translatie van \(f\). Je krijgt dan:
\(
\eqalign{
& P(p,p^2 ) \cr
& Q(p + 2,p^2 - 1) \cr
& a = \frac{{p^2 - 1 - p^2 }}
{{p + 2 - p}} = \frac{{ - 1}}
{2} = - \frac{1}
{2} \cr
& f'(p) = 2p = - \frac{1}
{2} \Rightarrow p = - \frac{1}
{4} \cr
& q = p + 2 = - \frac{1}
{4} + 2 = 1\frac{3}
{4} \cr}
\)
Maar ja... ga dat maar 's uitleggen dan...:-)
\( \eqalign{ & f(x) = x^2 \cr & g(x) = x^2 - 4x + 3 \cr} \)
De gemeenschappelijke raaklijn raakt \(f\) in \(x=p\) en \(g\) in \(x=q\).
- Bereken de waarde van \(p\) en \(q\).
Je kunt \(g\) opvatten als een translatie van \(f\). Je krijgt dan:
\(
\eqalign{
& P(p,p^2 ) \cr
& Q(p + 2,p^2 - 1) \cr
& a = \frac{{p^2 - 1 - p^2 }}
{{p + 2 - p}} = \frac{{ - 1}}
{2} = - \frac{1}
{2} \cr
& f'(p) = 2p = - \frac{1}
{2} \Rightarrow p = - \frac{1}
{4} \cr
& q = p + 2 = - \frac{1}
{4} + 2 = 1\frac{3}
{4} \cr}
\)
Maar ja... ga dat maar 's uitleggen dan...:-)
maandag 24 juni 2019
Elektriciteitsverbruik
Ik had op elektriciteitsverbruik in eerste instantie gebruik gemaakt van integralen. Dat was vooral vanwege de oorspronkelijke titel 'integralen' en de gekozen categorie 'integreren'. Maar, zoals @GHvD opmerkte, zat er wel een addertje onder het gras. Met het verbruik per jaar zou je moeten rekenen met discrete waarden.
Daar zit wat in. Uiteindelijk ben ik er wel uitgekomen, geloof ik, maar wat nu precies de bedoeling was zullen we nooit weten...
Formule
\(
\eqalign{
& V_{gemiddeld} = \frac{{S_{20} }}
{{20}} = \frac{{3\root {10} \of 2 \cdot v_0 }}
{{20(\root {10} \of 2 - 1)}} \cr}
\)
Voorbeeld
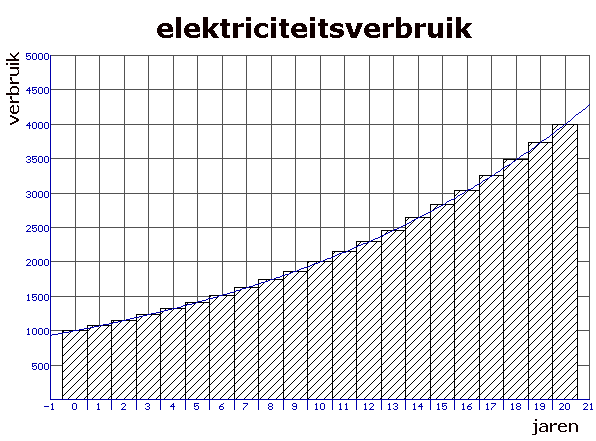
Neem \(v_0=1000\). In Excel krijg je dan zoiets als:
De formule hierboven geeft \(V_{gemiddeld}=2.239,9\) dus dat klopt...:-)
Hier kan je dan misschien toch nog wel iets doen met een integraal. Je moet wel even goed naar de grenzen kijken, maar dan heb je ook wat.
\(
\eqalign{V_{gemiddeld} = \frac{{\int\limits_{t = \frac{1}
{2}}^{20\frac{1}
{2}} {1000 \cdot e^{\frac{{\ln (2)}}
{{10}}t} dt} }}
{{20}} \approx 2240,4}
\)
Of, maar dan meer in het algemeen, voor een willekeurige waarde van \(v_0\):
\(
\eqalign{V_{gemiddeld} = v_0 \cdot \frac{{3 \cdot \root {20} \of 2 }}
{{2 \cdot \ln (2)}}}
\)
Ik bedoel maar. Ik vermaak me wel...:-)
Daar zit wat in. Uiteindelijk ben ik er wel uitgekomen, geloof ik, maar wat nu precies de bedoeling was zullen we nooit weten...
Formule
\(
\eqalign{
& V_{gemiddeld} = \frac{{S_{20} }}
{{20}} = \frac{{3\root {10} \of 2 \cdot v_0 }}
{{20(\root {10} \of 2 - 1)}} \cr}
\)
Voorbeeld
Neem \(v_0=1000\). In Excel krijg je dan zoiets als:
| jaar | verbruik |
| 1 | 1.072 |
| 2 | 1.149 |
| 3 | 1.231 |
| 4 | 1.320 |
| 5 | 1.414 |
| 6 | 1.516 |
| 7 | 1.625 |
| 8 | 1.741 |
| 9 | 1.866 |
| 10 | 2.000 |
| 11 | 2.144 |
| 12 | 2.297 |
| 13 | 2.462 |
| 14 | 2.639 |
| 15 | 2.828 |
| 16 | 3.031 |
| 17 | 3.249 |
| 18 | 3.482 |
| 19 | 3.732 |
| 20 | 4.000 |
| gemiddeld | 2.240 |
De formule hierboven geeft \(V_{gemiddeld}=2.239,9\) dus dat klopt...:-)
Hier kan je dan misschien toch nog wel iets doen met een integraal. Je moet wel even goed naar de grenzen kijken, maar dan heb je ook wat.
\(
\eqalign{V_{gemiddeld} = \frac{{\int\limits_{t = \frac{1}
{2}}^{20\frac{1}
{2}} {1000 \cdot e^{\frac{{\ln (2)}}
{{10}}t} dt} }}
{{20}} \approx 2240,4}
\)
Of, maar dan meer in het algemeen, voor een willekeurige waarde van \(v_0\):
\(
\eqalign{V_{gemiddeld} = v_0 \cdot \frac{{3 \cdot \root {20} \of 2 }}
{{2 \cdot \ln (2)}}}
\)
Ik bedoel maar. Ik vermaak me wel...:-)
dinsdag 29 mei 2018
maandag 21 mei 2018
WisFaq
zaterdag 19 mei 2018
dinsdag 8 mei 2018
donderdag 12 april 2018
Herleiden
\(
\eqalign{
& 27^{ - \frac{x}
{3}} + 81^{\frac{{1 - x}}
{4}} = \cr
& \left( {3^3 } \right)^{ - \frac{x}
{3}} + \left( {3^4 } \right)^{\frac{{1 - x}}
{4}} = \cr
& 3^{3 \cdot - \frac{x}
{3}} + 3^{4 \cdot \frac{{1 - x}}
{4}} = \cr
& 3^{ - x} + 3^{1 - x} = \cr
& 3^{ - x} + 3 \cdot 3^{ - x} = \cr
& 4 \cdot 3^{ - x} = \cr
& \frac{4}
{{3^x }} \cr}
\)
vrijdag 6 april 2018
Heldere momenten
Kort samengevat: het curriculum voor #wiskunde is volstrekt van ondergeschikt belang. Ik heb de laatste 30 jaar allerlei wijziging van dichtbij meegemaakt en 't maakt allemaal geen **** uit... Het gaat om de groenten niet om het paard-en-wagen... #jippie
...en voor de jeugd... de groenteman kwam vroeger door de straat met een paard en wagen... dat weet ik nog wel...:-) google.nl/search?q=de+pa…
...alhoewel.... het kan ook de schillenboer zijn geweest... :-)
Ik had me nog zo voorgenomen me niet te bemoeien met dat @Curriculum_nu - maar ja... af en toe heb ik ook zwakke momenten...:-)
...en voor de jeugd... de groenteman kwam vroeger door de straat met een paard en wagen... dat weet ik nog wel...:-) google.nl/search?q=de+pa…
...alhoewel.... het kan ook de schillenboer zijn geweest... :-)
Ik had me nog zo voorgenomen me niet te bemoeien met dat @Curriculum_nu - maar ja... af en toe heb ik ook zwakke momenten...:-)
dinsdag 3 april 2018
Week 22
In een natuurgebied worden vijf jonge dieren van een bedreigde soort losgelaten. Ieder diertje heeft een kans van 90% om te overleven in het eerste jaar. Pas na het eerste jaar zijn de dieren geslachtsrijp, en er waren vooraf geen andere dieren van dezelfde soort aanwezig in het gebied.Na het eerste jaar wil men nagaan hoeveel dieren nog in leven zijn. Daartoe vangt men het eerste dier dat men tegenkomt, om het te merken en dan weer los te laten. Een week later herhaalt men die procedure op een andere plaats in het gebied. Het eerste dier dat men tegenkomt blijkt het gemerkte dier te zijn.
- Hoe groot is de kans dat ten minste 1 van de dieren gestorven is?
maandag 26 februari 2018
Drie punten op een lijn
Gegeven: zijn drie punten op een lijn A( 19, -8), B(13, 1) en C(9, c).
\(
\eqalign{
& a = \frac{{1 - - 8}}
{{13 - 19}} = \frac{9}
{{ - 6}} = - 1\frac{1}
{2} \cr
& y = - 1\frac{1}
{2}\left( {x - 9} \right) + c \cr
& 1 = - 1\frac{1}
{2}\left( {13 - 9} \right) + c \cr
& c = 7 \cr}
\)
- Bereken c.
- Hoe zou je dat (handig) berekenen?
\(
\eqalign{
& a = \frac{{1 - - 8}}
{{13 - 19}} = \frac{9}
{{ - 6}} = - 1\frac{1}
{2} \cr
& y = - 1\frac{1}
{2}\left( {x - 9} \right) + c \cr
& 1 = - 1\frac{1}
{2}\left( {13 - 9} \right) + c \cr
& c = 7 \cr}
\)
zaterdag 24 februari 2018
Ook leuk
\(
\eqalign{
& \left( {\sqrt {3 + \sqrt 5 } + \sqrt {3 - \sqrt 5 } } \right)^2 \cr
& 3 + \sqrt 5 + 2\sqrt {3 + \sqrt 5 } \cdot \sqrt {3 - \sqrt 5 } + 3 - \sqrt 5 \cr
& 6 + 2\sqrt {3 + \sqrt 5 } \cdot \sqrt {3 - \sqrt 5 } \cr
& 6 + 2\sqrt {9 - 5} \cr
& 6 + 2\sqrt 4 \cr
& 10 \cr}
\)
vrijdag 16 februari 2018
Voorkennis, algebra, probleemaanpak, begrip en inzicht
Op Weekpuzzels 2017 deel 2 stond een aardige opgave:
Op Oplossing week 23 staat ook een uitwerkingen van de oplossing. Op de uitwerking van de Wiskunde Academie was nog wel iets op te merken in het kader van wortels in de noemer.
De vraag is nu 'hoe pak je deze opgave aan?' en met welk 'begrip en inzicht' hebben we hier van doen?
Aanpak
In de oplossing staat niets over hoe je deze opgave aanpakt. Kennelijk heb ik iets gedaan met verhoudingen. Maar hoe kom je er op?
Voor het berekenen van de oppervlakte heb ik de lengte van een zijde en de bijbehorende hoogte nodig. Als AB=8 en ik zou de lengte van CD kennen dan was ik er al. Maar CD ken ik niet dus laat ik de lengte van CD dan x noemen.
Als CD=x dan is AD=x wegens de 45-45-90-tekendriehoek ADC. Je kunt nu DB uitdrukken in x zodat je in de 30-60-90-driehoek DBC de twee rechthoekszijden kan uitdrukken in x. In zo'n driehoek ken ik immers de verhoudingen van de zijden.
Die eigenschappen van de tekendriehoeken is de kennis die je nodig hebt. De aanpak is om vanuit de kennis een plan te maken. Wat weet ik eigenlijk van rechthoekige driehoeken met de hoeken zoals die gegeven zijn...
Je kunt nu een verhoudingstabel opstellen voor driehoek DBC. Met DB=8-x en CD=x in de verhouding 1:√3 kan je waarde van x berekenen. De oppervlakte van driehoek ABC volgt spoedig daarna...:-)
Begrip en inzicht
De oppervlakte van een willekeurige driehoek, werken met tekendriehoeken, een vergelijking opstellen, vergelijkingen oplossen, rekenen met wortels, ... Als dat allemaal lukt ben je (als docent) waarschijnlijk al blij. In dat geval zijn als die wiskundelessen niet voor niets geweest.
In de praktijk doen zich mogelijkerwijs de volgende problemen voor:
Voorkennis
Je zou de voorkennis kunnen indelen in kennen, kunnen en begrijpen. Je moet begrijpen wat de oppervlakte van een driehoek is, hoe je, bij gegeven afmetingen, de oppervlakte uit zou kunnen rekenen en misschien moet je ook de formule wel kennen. Iets met tekendriehoeken... een portie algebra... maar... waarschijnlijk is het veel belangrijker hoe je dit soort problemen aan kan pakken.
Probleemaanpak
Bij probleemaanpak zet je de instrumenten in die je in de onderbouw hebt geleerd. Dat was het plan. De kunst is om te herkennen hoe je je probleem kunt vertalen naar wiskunde, vervolgens aan de slag met de wiskunde om het probleem op te lossen om vervolgens je oplossing te vertalen naar je probleem. Daar is NIETS mis mee. Op dit weblog kan je daar meer over vinden.
Algebra
Als je eenmaal op de juiste uitdrukking bent gekomen dan kan je de zaak verder uitwerken. Die (algebraische) vaardigheden die je daar voor nodig hebt zouden (halverwege de 4e klas) aanwezig moeten zijn.
Conclusie
Voor dit soort opgave is er heel wat nodig aan kennis en vaardigheden. Het zijn (volgens mij) complexe bezigheden. Hier komt alles samen: kennen, kunnen en begrijpen. Inderdaad, maar hoe kan je dat leren? Dat is niet zo eenvoudig als sommigen van ons willen doen geloven. Het gaat niet alleen om algebraische vaardigheden, maar ook over probleemaanpak, atitude en begrip en inzicht. Wat is hier geboden? Hoe pak ik dit aan? Wat zit er achter? Hoe kan je dat leren?
Op Oplossing week 23 staat ook een uitwerkingen van de oplossing. Op de uitwerking van de Wiskunde Academie was nog wel iets op te merken in het kader van wortels in de noemer.
De vraag is nu 'hoe pak je deze opgave aan?' en met welk 'begrip en inzicht' hebben we hier van doen?
Aanpak
In de oplossing staat niets over hoe je deze opgave aanpakt. Kennelijk heb ik iets gedaan met verhoudingen. Maar hoe kom je er op?
Voor het berekenen van de oppervlakte heb ik de lengte van een zijde en de bijbehorende hoogte nodig. Als AB=8 en ik zou de lengte van CD kennen dan was ik er al. Maar CD ken ik niet dus laat ik de lengte van CD dan x noemen.
Als CD=x dan is AD=x wegens de 45-45-90-tekendriehoek ADC. Je kunt nu DB uitdrukken in x zodat je in de 30-60-90-driehoek DBC de twee rechthoekszijden kan uitdrukken in x. In zo'n driehoek ken ik immers de verhoudingen van de zijden.
Die eigenschappen van de tekendriehoeken is de kennis die je nodig hebt. De aanpak is om vanuit de kennis een plan te maken. Wat weet ik eigenlijk van rechthoekige driehoeken met de hoeken zoals die gegeven zijn...
Je kunt nu een verhoudingstabel opstellen voor driehoek DBC. Met DB=8-x en CD=x in de verhouding 1:√3 kan je waarde van x berekenen. De oppervlakte van driehoek ABC volgt spoedig daarna...:-)
Begrip en inzicht
De oppervlakte van een willekeurige driehoek, werken met tekendriehoeken, een vergelijking opstellen, vergelijkingen oplossen, rekenen met wortels, ... Als dat allemaal lukt ben je (als docent) waarschijnlijk al blij. In dat geval zijn als die wiskundelessen niet voor niets geweest.
In de praktijk doen zich mogelijkerwijs de volgende problemen voor:
- De leerlingen lijken niet de beschikking te hebben over de noodzakelijk kennis uit de onderbouw
- Leerlingen hebben niet geleerd om problemen aan te pakken
- Leerlingen lopen vast op de algebra
Voorkennis
Je zou de voorkennis kunnen indelen in kennen, kunnen en begrijpen. Je moet begrijpen wat de oppervlakte van een driehoek is, hoe je, bij gegeven afmetingen, de oppervlakte uit zou kunnen rekenen en misschien moet je ook de formule wel kennen. Iets met tekendriehoeken... een portie algebra... maar... waarschijnlijk is het veel belangrijker hoe je dit soort problemen aan kan pakken.
Probleemaanpak
Bij probleemaanpak zet je de instrumenten in die je in de onderbouw hebt geleerd. Dat was het plan. De kunst is om te herkennen hoe je je probleem kunt vertalen naar wiskunde, vervolgens aan de slag met de wiskunde om het probleem op te lossen om vervolgens je oplossing te vertalen naar je probleem. Daar is NIETS mis mee. Op dit weblog kan je daar meer over vinden.
Algebra
Als je eenmaal op de juiste uitdrukking bent gekomen dan kan je de zaak verder uitwerken. Die (algebraische) vaardigheden die je daar voor nodig hebt zouden (halverwege de 4e klas) aanwezig moeten zijn.
Conclusie
Voor dit soort opgave is er heel wat nodig aan kennis en vaardigheden. Het zijn (volgens mij) complexe bezigheden. Hier komt alles samen: kennen, kunnen en begrijpen. Inderdaad, maar hoe kan je dat leren? Dat is niet zo eenvoudig als sommigen van ons willen doen geloven. Het gaat niet alleen om algebraische vaardigheden, maar ook over probleemaanpak, atitude en begrip en inzicht. Wat is hier geboden? Hoe pak ik dit aan? Wat zit er achter? Hoe kan je dat leren?
maandag 5 februari 2018
Ontbinden in factoren
\(
\eqalign{
& 3x^2 + 4x + 1 \cr
& 3x^2 + x + 3x + 1 \cr
& 3x(x + 1) + 3x + 1 \cr
& (3x + 1)(x + 1) \cr}
\)
dinsdag 5 december 2017
Dat kan ook...
\(
\eqalign{
& x^2 - 5x + 2\frac{3}
{4} = 0 \cr
& 4x^2 - 20x + 11 = 0 \cr
& \left( {2x - 5} \right)^2 - 25 + 11 = 0 \cr
& (2x - 5)^2 - 14 = 0 \cr
& 2x - 5 = \pm \sqrt {14} \cr
& x = 2\frac{1}
{2} - \sqrt {14} \vee x = 2\frac{1}
{2} + \sqrt {14} \cr}
\)
zondag 9 april 2017
zondag 19 maart 2017
Week 12
Wat is de kans dat je uit een volledig kaartspel (zonder terugleggen) eerst een schoppen kaart trekt en dan een heer?
maandag 2 januari 2017
Fib(1001)
Fib(1001)=70330367711422815821835254877183549770181269836358732742604905087154537118196933579742249494562611733487750449241765991088186363265450223647106012053374121273867339111198139373125598767690091902245245323403501
zaterdag 10 december 2016
maandag 28 november 2016
Abonneren op:
Posts (Atom)