Hoe oud is tante Annie?

Tante Annie zegt: 'Over 12 jaar ben ik drie keer zo oud als 48 jaar geleden' Stel een vergelijking op en bereken hoe oud tante Annie is.

• Hoe oud is tante Annie?

Tante Annie is 78 jaar oud...👅

Goniometrische functie

Logaritmische standaardfunctie

Volgens mij is de logaritmische standaardfunctie gegeven door:

\( f(x) = a + b \ln (x - c) \)

Dat zou voldoende moeten zijn om bij twee gegeven punten een functievoorschrift op te stellen. Daar houd ik het voorlopig maar even op.👅

• De grafiek bekijken in Desmos

\( \eqalign{f(x) = 2 + \frac{1} {{\ln (4)}}\ln (x + 2)} \)

Functievoorschrift logaritmische functie

De grafiek van de logaritmische functie y=a·⁴log(x + b) gaat door de punten (2,0) en (12,4).

• Bepaal a en b.

• De grafiek bekijken in Desmos

Functievoorschrift opstellen

• Functievoorschrift opstellen

Dudeney's haberdasher puzzel

Dat is een leuke benadering!

• Dudeney's haberdasher puzzel

De som van de kwadraten

Op WisFaq kwam ik deze vraag tegen:

"Wat is de som van de kwadraten van de diagonalen van een ruit met zijde 4?"

De diagonalen staan loodrecht op elkaar en delen elkaar middendoor. Met a en b als lengten van de halve diagonalen dan geldt:

\(
a^2  + b^2 = 16
\)

Zodat de som van de kwadraten \(S\) gelijk is aan:

\(
\eqalign{
  & S = \left( {2a} \right)^2  + \left( {2b} \right)^2   \cr
  & S = 4a^2  + 4b^2   \cr
  & S = 4(a^2  + b^2 )  \cr
  & S = 4 \cdot 16  \cr
  & S = 64 \cr}
\)

...en dat is dan wel weer aardig...👅

Zie:

§ 12. Van elk parallelogram, elke ruit, is de som der kwadraten van de zijden gelijk aan de som der kwadraten van de diagonalen.
MEETKUNDIG SCHOOLBOEK.DOOR H. SLUIJTERS. 1848

• Zie ook de Parallellogramwet op Wikipedia

Je kan deze vraag ook als meerkeuzevraag tegen komen in de Voorbereiding toelatingsexamen arts/tandarts -  Wiskunde: goniometrie en meetkunde. Dat is dan toch wel weer hoopgevend...👀

Zo'n jaar of zes geleden ging er bij het stellen van deze vraag kennelijk iets niet helemaal goed, maar uiteindelijk wordt zoiets dan toch opgelost.

• Som diagonaal ruit
  

Bewijzen van gelijkheden

A

Naar aanleiding van Bewijzen van gelijkheden:

Opdracht 1

\(
\eqalign{
  & \cos \alpha  \cdot \left( {\tan \alpha  + 2} \right) \cdot \left( {2\tan \alpha  + 1} \right) = \frac{2}
{{\cos \alpha }} + 5\sin \alpha   \cr  
  & \left( {\tan \alpha  + 2} \right) \cdot \left( {2\tan \alpha  + 1} \right) = \frac{2}
{{\cos ^2 \alpha }} + 5\tan \alpha   \cr  
  & 2\tan ^2 \alpha  + 5\tan \alpha  + 2 = \frac{2}
{{\cos ^2 \alpha }} + 5\tan \alpha   \cr  
  & 2\tan ^2 \alpha  + 2 = \frac{2}
{{\cos ^2 \alpha }}  \cr  
  & \frac{{\sin ^2 \alpha }}
{{\cos ^2 \alpha }} + 1 = \frac{1}
{{\cos ^2 \alpha }}  \cr  
  & \frac{{\sin ^2 \alpha }}
{{\cos ^2 \alpha }} + \frac{{\cos ^2 \alpha }}
{{\cos ^2 \alpha }} = \frac{1}
{{\cos ^2 \alpha }}  \cr  
  & \frac{{\sin ^2 \alpha  + \cos ^2 \alpha }}
{{\cos ^2 \alpha }} = \frac{1}
{{\cos ^2 \alpha }}  \cr  
  & \frac{1}
{{\cos ^2 \alpha }} = \frac{1}
{{\cos ^2 \alpha }} \cr}  
\) 

Opdracht 2

\(
\eqalign{
  & \frac{1}
{{1 - \sin \alpha }} + \frac{1}
{{1 + \sin \alpha }} = \frac{2}
{{\cos ^2 \alpha }}  \cr
  & \frac{1}
{{1 - \sin \alpha }} \cdot \frac{{1 + \sin \alpha }}
{{1 + \sin \alpha }} + \frac{1}
{{1 + \sin \alpha }} \cdot \frac{{1 - \sin \alpha }}
{{1 - \sin \alpha }} = \frac{2}
{{\cos ^2 \alpha }}  \cr
  & \frac{{1 + \sin \alpha  + 1 - \sin \alpha }}
{{1 - \sin ^2 \alpha }} = \frac{2}
{{\cos ^2 \alpha }}  \cr
  & \frac{2}
{{1 - \sin ^2 \alpha }} = \frac{2}
{{\cos ^2 \alpha }}  \cr
  & \frac{2}
{{\cos ^2 \alpha }} = \frac{2}
{{\cos ^2 \alpha }} \cr}
\)

Bij wiskunde komt altijd alles wel weer ergens terug...:-)

Puzzeltje

Op Facebook kom je ze nog wel 's tegen, een soort van puzzeltjes. Veel nut heeft dat niet. 

\( \begin{array}{l} 1 + 4 = 5 \\ 2 + 5 = 12 \\ 3 + 6 = 21 \\ ... \\ 8 + 11 = ? \\ \end{array} \) 

 Maar ja... Ik zou denken dat het \(96\) moet zijn.👅

Hoe moeilijk kan 't zijn?

\( \eqalign{ & f(x) = x\root 3 \of {(x^3 + 3x)^2 } \cr & f(x) = x\left( {x{}^3 + 3x} \right)^{\frac{2} {3}} \cr & f'(x) = 1 \cdot \left( {x{}^3 + 3x} \right)^{\frac{2} {3}} + x \cdot \frac{2} {3}\left( {x{}^3 + 3x} \right)^{ - \frac{1} {3}} \cdot \left( {3x^2 + 3} \right) \cr & f'(x) = \left( {x{}^3 + 3x} \right)^{\frac{2} {3}} + \frac{{2x\left( {3x^2 + 3} \right)}} {{3\left( {x{}^3 + 3x} \right)^{\frac{1} {3}} }} \cr & f'(x) = \left( {x{}^3 + 3x} \right)^{\frac{2} {3}} \cdot \frac{{3\left( {x{}^3 + 3x} \right)^{\frac{1} {3}} }} {{3\left( {x{}^3 + 3x} \right)^{\frac{1} {3}} }} + \frac{{2x\left( {3x^2 + 3} \right)}} {{3\left( {x{}^3 + 3x} \right)^{\frac{1} {3}} }} \cr & f'(x) = \frac{{3(x{}^3 + 3x)}} {{3\left( {x{}^3 + 3x} \right)^{\frac{1} {3}} }} + \frac{{2x\left( {3x^2 + 3} \right)}} {{3\left( {x{}^3 + 3x} \right)^{\frac{1} {3}} }} \cr & f'(x) = \frac{{3x^3 + 9x + 6x^3 + 6x}} {{3\left( {x{}^3 + 3x} \right)^{\frac{1} {3}} }} \cr & f'(x) = \frac{{9x^3 + 15x}} {{3\left( {x{}^3 + 3x} \right)^{\frac{1} {3}} }} \cr & f'(x) = \frac{{3x^3 + 5x}} {{\root 3 \of {x{}^3 + 3x} }} \cr} \)

Ook leuk

\( \eqalign{ & g(x) = \frac{{\sin (x)}} {{\frac{1} {2} - \cos (x)}} \cr & g'(x) = \frac{{\cos (x)\left( {\frac{1} {2} - \cos (x)} \right) - \sin (x) \cdot \sin (x)}} {{\left( {\frac{1} {2} - \cos (x)} \right)^2 }} \cr & g'(x) = \frac{{\frac{1} {2}\cos (x) - \cos ^2 (x) - \sin ^2 (x)}} {{\left( {\frac{1} {2} - \cos (x)} \right)^2 }} \cr & g'(x) = \frac{{\frac{1} {2}\cos (x) - 1}} {{\left( {\frac{1} {2} - \cos (x)} \right)^2 }} \cr} \) 

Of ook...

 \( \eqalign{ & g(x) = \frac{{2 \cdot \sin (x)}} {{1 - 2 \cdot \cos (x)}} \cr & g'(x) = \frac{{2 \cdot \cos (x)(1 - 2 \cdot \cos (x)) - 2 \cdot \sin (x) \cdot 2 \cdot \sin (x)}} {{\left( {1 - 2 \cdot \cos (x)} \right)^2 }} \cr & g'(x) = \frac{{2 \cdot \cos (x) - 4 \cdot \cos ^2 (x) - 4 \cdot \sin ^2 (x)}} {{\left( {1 - 2 \cdot \cos (x)} \right)^2 }} \cr & g'(x) = \frac{{2 \cdot \cos (x) - 4}} {{\left( {1 - 2 \cdot \cos (x)} \right)^2 }} \cr} \)

Wat zal ik er van denken?:-)
Wat zal het programma er over denken?:-)
Ik zeg niks...:-)

Alsof het allemaal niks kost...:-)

 

Nog meer maffe grafieken

• Desmos

Afstandsformule

Ik van wel een beetje in herhaling met die afstandsformule voor een punt en een lijn:

• Oefening 37
• Oefening 38
• Oefening 40
• Oefening 41
• Oefening 42
• Oefening 43
• Oefening 45

Maar je moet wat...

Naschrift
Of had ik dat al gezegd?:-)

Oefening 39

Bepaal de vergelijking(en) van de rechte(n) evenwijdig met de rechte a:x-2y+1=0 en op een afstand 3 ervan. 

Uitwerking

Gebruik de afstandsformule van een punt en een lijn: 

\(
\eqalign{
  & A(a,b)  \cr
  & k:px + qy + r = 0  \cr
  & d(A,k) = \frac{{\left| {pa + qy + r} \right|}}
{{\sqrt {p^2  + q^2 } }} \cr}
\)

Geeft:

\(
\eqalign{
  & A(1,1)  \cr
  & k:x - 2y + r = 0  \cr
  & d(A,k) = \frac{{\left| {1 - 2 + r} \right|}}
{{\sqrt {1^2  + \left( { - 2} \right)^2 } }} = \frac{{\left| {r - 1} \right|}}
{{\sqrt 5 }} = 3 \cr}
\)

Kan ook...👅

• Zie ook Afstandsformule

Dat begint op werk te lijken...

Stel een passend functievoorschrift op (2)

 Uit HAVO wiskunde B hoofdstuk 14:

Dat is een mooi idee. De vraag wordt geleid en leidt uiteindelijk tot:

Dat is (op zich) prima, maar in het licht van de gekozen didactiek ligt de formule voor de sinus niet helemaal voor de hand. Als je voor c de waarde kiest waar bij de grafiek stijgend door de evenwichtsstand gaat dan zou ik geneigd zijn het punt \((1\frac{3}{4}\pi,0)\) te nemen:

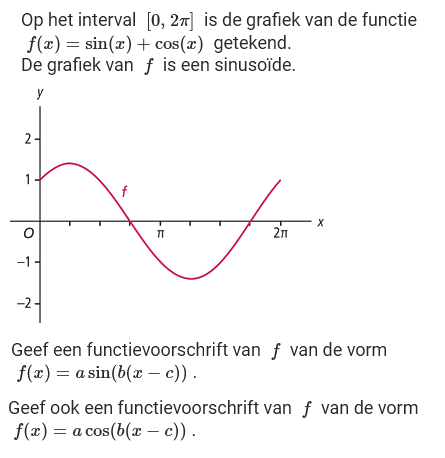
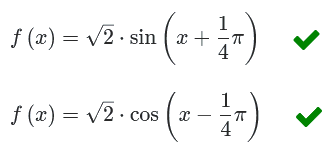
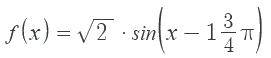
De vraag is nu: zou het programma dat goed vinden?👅

HAVO wiskunde B hoofdstuk 14 - Test jezetf 4

Stel een passend functievoorschrift op

Uit HAVO wiskunde B hoofdstuk 14:

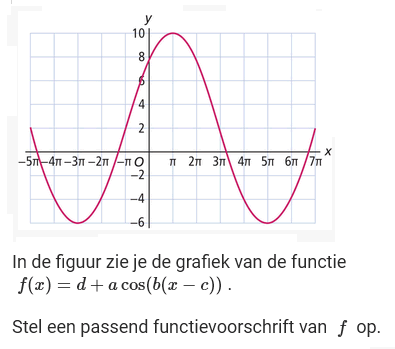
Het gaat hier om cosinus dus voor de waarde van c zoek je een top met een maximum. Het punt \((\pi,10)\) ligt voor de hand. Waarschijnlijk zal het antwoord geen problemen geven:

Maar bij de tweede opgave moet je toch even opletten...

Normale mensen zullen waarschijnlijk kiezen voor de sinus. Je krijgt dan:

Dat is natuurlijk prima. Je hebt een punt waarbij de grafiek stijgend door de evenwichtsstand gaat dus neem de sinus met c=4. Maar je kunt ook de cosinus nemen:

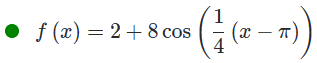
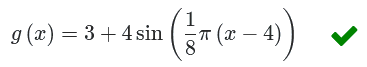
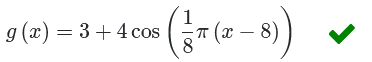
Dat kan ook... maar dat antwoord moet je er dan wel apart inzetten. Het programma zou het in eerste instantie niet goed rekenen.

HAVO B hoofdstuk 14 - Extra oefening E1

Een wikkel van een suikerklontje

"Op een wikkel van een suikerklontje staat op zes verschillende plaatsen in zes verschillende talen het woord suiker. Er wordt gekozen uit tien talen waaronder Nederlands. Hoeveel verschillende wikkels zijn er mogelijk waarop je het woord 'suiker' aantreft?"

• Re: Re: Permutaties

Uitgewerkt:-)

\( \left( {10} \right)_6 - \left( 9 \right)_6 = {\rm{151}}{\rm{.200 - 60}}{\rm{.480 = 90}}{\rm{.720}} \)

Boxplot

Dataset

Eén 6 als kleinste getal.
Dan 26 keer een willekeurig getal tussen 6 en 8,1.
Een 8,1 voor de mediaan.
Dan 26 keer een willekeuirg getal tussen 8,1 en 9.
En tenslotte één 9 als grootste getal.

Boxplot

• Boxplot naar getallen

Nog meer verhoudingen...

Nog meer verhoudingen bij Lengte ribben berekenen. Hoe pak je zoiets aan? 't Is een monster...

\( \eqalign{ & a:b:c = 4(a + b + c):2(ab + ac + bc):abc \cr & I. \cr & a:c = 4(a + b + c):abc \cr & c = \frac{{a^2 b - 4a - 4b}} {4} \cr & II. \cr & b:c = 2(ab + ac + bc):abc \cr & c = \frac{{ab(b - 2)}} {{2(a + b)}} \cr & Geeft: \cr & \frac{{a^2 b - 4a - 4b}} {4} = \frac{{ab(b - 2)}} {{2(a + b)}} \cr & a^2 b - 4a - 4b = \frac{{2ab(b - 2)}} {{a + b}} \cr & (a^2 b - 4a - 4b)(a + b) = 2ab(b - 2) \cr & a^3 b - 4a^2 - 4ab + a^2 b^2 - 4b^2 - 2ab^2 = 0 \cr & \left( {a^2 - 2a - 4} \right)b^2 + \left( {a^3 - 4a} \right)b - 4a^2 = 0 \cr & b^2 + \frac{{a^3 - 4a}} {{a^2 - 2a - 4}}b - \frac{{4a^2 }} {{a^2 - 2a - 4}} = 0 \cr & \left( {b + \frac{{a^3 - 4a}} {{2a^2 - 4a - 8}}} \right)^2 - \left( {\frac{{a^3 - 4a}} {{a^2 - 2a - 4}}} \right)^2 - \frac{{4a^2 }} {{a^2 - 2a - 4}} = 0 \cr & \left( {b + \frac{{a^3 - 4a}} {{2a^2 - 4a - 8}}} \right)^2 - \frac{{a^6 - 4a^4 - 8a^3 }} {{\left( {a^2 - 2a - 4} \right)^2 }} = 0 \cr & b = - \frac{{a^3 - 4a}} {{2a^2 - 4a - 8}} \pm \sqrt {\frac{{a^6 - 4a^4 - 8a^3 }} {{\left( {a^2 - 2a - 4} \right)^2 }}} \cr} \)

---

• Lengte ribben berekenen

---

Verhoudingen

Bij zo'n vraag als De lengte van ribben van een balk berekenen is het altijd even de vraag hoe je verhoudingen kunt vertalen naar vergelijkingen. Vergelijkingen kan je in een stelsel van vergelijkingen zetten en fijn oplossen. Of nog beter: laat ze oplossen...😀

In het geval van bovenstand probleem zou dat zo kunnen:

\( \begin{array}{l} ab:ac:bc = 1:5:10 \\ \frac{{ab}}{{ac}} = \frac{1}{5} \Rightarrow \frac{b}{c} = \frac{1}{5} \Rightarrow 5b = c \\ \frac{{ab}}{{bc}} = \frac{1}{{10}} \Rightarrow \frac{a}{c} = \frac{1}{{10}} \Rightarrow 10a = c \\ \left\{ \begin{array}{l} abc = 160 \\ 5b = c \\ 10a = c \\ \end{array} \right. \Rightarrow \left\{ \begin{array}{l} a = 2 \\ b = 4 \\ c = 20 \\ \end{array} \right. \\ \end{array} \)

Uitgewerkt:

\( \begin{array}{l} \left\{ \begin{array}{l} abc = 160 \\ b = \frac{1}{5}c \\ a = \frac{1}{{10}}c \\ \end{array} \right. \Rightarrow \\ \frac{1}{{10}}c \cdot \frac{1}{5}c \cdot c = 160 \\ \frac{1}{{50}}c^3 = 160 \\ c^3 = 8000 \\ c = 20 \\ \left\{ \begin{array}{l} a = 2 \\ b = 4 \\ c = 20 \\ \end{array} \right. \\ \end{array} \)

Als je dat kan dan kan je Lengte ribben berekenen ook 's proberen...👅

De wijzers van de klok

Naar aanleiding van Hoe bereken je de hoek tussen de wijzers van de klok?

 

\( \eqalign{ & y:x\,\,\,uur \cr & \alpha = 6x \cr & \beta = 360 - \frac{1} {2}\left( {60y + x} \right) \cr & \alpha = \beta \cr & 6x = 360 - \frac{1} {2}\left( {60y + x} \right) \cr & 6x = 360 - 30y - \frac{1} {2}x \cr & 6\frac{1} {2}x = 360 - 30y \cr & 13x = 720 - 60y \cr & x = \frac{{720 - 60y}} {{13}} \cr} \) 

Enz...👅

Soms levert een antwoord in WisFaq van allerlei ideetjes op. Dit is wel een geschikt probleem voor probleemaanpak. Je kunt zelfs randomizeren met de uren. In het voorbeeld ging het om een tijd tussen 10 en 11, maar je kan natuurlijk ook bij andere tijden kijken. 

Je weet maar nooit wanneer dat weer 's van pas komt. Om maar 's wat te noemen, qua opbrengsten. Voor de rest moet ik er nog maar 's over nadenken...  over het conceptueel strategisch beleidsplan, zullen we maar zeggen...

Lesbrief hypergeometrische verdeling

Inhoudsopgave

• Inhoudsopgave
• Hoofdstuk 1 - Laplace
• Hoofdstuk 2 - de hypergeometrische verdeling
• Hoofdstuk 3 - wanneer gebruik je welke verdeling? 
• Hoofdstuk 4 - extra opgaven 

Lesbrieven

• Lesbrief normale verdeling
  Van de ‘oude’ cursus statistiek 2-1
• Lesbrief hypothesetoetsen
  Van de ‘oude’ cursus statistiek 2-2
• Lesbrief Poisson verdeling
  Verkorte route Zebraboekje
• Lesbrief hypergeometrische verdeling
  Aanvullende materialen van ‘statistiek 1-2
  

Lesbrief Poisson-verdeling

Inhoudsopgave

• Voorkennis
• Hoofdstuk 1 - wiskundige afleiding van de Poissonverdeling 
• Hoofdstuk 2 - voorbeelden
• Hoofdstuk 3 - waargenomen en berekende waarden 
• Hoofdstuk 4 - verjaardagsproblemen
• Hoofdstuk 5 - het dekpuntenprobleem
• Uitwerkingen van de opgaven

Lesbrieven

• Lesbrief normale verdeling
  Van de ‘oude’ cursus statistiek 2-1
• Lesbrief hypothesetoetsen
  Van de ‘oude’ cursus statistiek 2-2
• Lesbrief Poisson verdeling
  Verkorte route Zebraboekje
• Lesbrief hypergeometrische verdeling
  Aanvullende materialen van ‘statistiek 1-2
  

Lesbrief hypothese toetsen

Inhoudsopgave

• Inhoudsopgave
  
• Hoofdstuk 1 - voorkennis
• Hoofdstuk 2 - mens erger je niet
• Hoofdstuk 3 - hypothese toetsen
• Hoofdstuk 4 - de tekentoets
• Hoofdstuk 5 - toetsen van het gemiddelde van een normaal verdeelde stochast
• Uitwerkingen van de opdrachten

Lesbrieven

• Lesbrief normale verdeling
  Van de ‘oude’ cursus statistiek 2-1
• Lesbrief hypothesetoetsen
  Van de ‘oude’ cursus statistiek 2-2
• Lesbrief Poisson verdeling
  Verkorte route Zebraboekje
• Lesbrief hypergeometrische verdeling
  Aanvullende materialen van ‘statistiek 1-2

Lesbrief de normale verdeling

Inhoudsopgave 

• Inhoudsopgave
• Hoofdstuk 1 – de normale verdeling
• De standaard normale verdeling
• Van normaal naar standaardnormaal
• Met de grafische rekenmachine
• Oefeningen
• Uitwerkingen van de oefeningen
  
• Hoofdstuk 2 – meer over de normale verdeling
• Normaal waarschijnlijkheidspapier
• Centrale limietstelling
• Benaderen binomiale verdeling
• Continuïteitscorrectie
• Oefeningen
• Uitwerkingen van de oefeningen
• Hoofdstuk 3 – de √n-wet
• De som van n onafhankelijke stochasten
• Het gemiddelde van n onafhankelijk stochasten
• Oefeningen
• Uitwerkingen van de oefeningen
• Hoofdstuk 4 – experiment
• Einde
• Tabel normale verdeling
• Inhoudsopgave compleet 

 Lesbrieven

• Lesbrief normale verdeling
  Van de ‘oude’ cursus statistiek 2-1
• Lesbrief hypothesetoetsen
  Van de ‘oude’ cursus statistiek 2-2
• Lesbrief Poisson verdeling
  Verkorte route Zebraboekje
• Lesbrief hypergeometrische verdeling
  Aanvullende materialen van ‘statistiek 1-2’
  

Drie dobbelstenen

In WisFaq kwam ik een vraag tegen over het gooien met drie dobbelstenen. Ik was op zoek naar een 'handige manier' om uit te rekenen wat de kans is dat je met drie dobbelstenen meer dan 11 gooit. Dat lijkt lastiger dan het is. 

Er zijn in totaal 16 verschillende uitkomsten als je kijkt naar de som van de ogen een worp met drie dobbelstenen. De gevraagde kans verdeelt die verschillende 'sommen' in twee gebeurtenissen A en B.

• A: 3 t/m 11
• B: 12 t/m 18

 De vraag is dan: wat is P(A) en P(B)?

Je weet al dat de kans om 3 t/m 10 te gooien gelijk is aan een \(\frac{1}{2}\). Daar komt dan de kans om 11 te gooien bij. Wat is P(11)?

Er zijn 216 mogelijke manieren om met 3 dobbelstenen te gooien. Bij hoeveel manieren is de som van de ogen gelijk aan 11?

• 1-4-6 kan op 6 manieren
• 1-5-5 kan op 3 manieren
• 2-3-6 kan op 6 manieren
• 2-4-5 kan op 6 manieren
• 3-3-5 kan op 3 manieren
• 3-4-4 kan op 3 manieren

Dat zijn 27 manieren om 11 te gooien. De kans P(11)=\(\frac{27}{216}=\frac{1}{8}\) 

Conclusie: P(A)=\( \frac{5}{8}\) en P(B)=\(\frac{3}{8}\)

• U. Is dit een eerlijk spel?

666

\( \sum\limits_{k = 1}^{36} k = 666 \)

Kansen en intervallen

Opgave

Je hebt een getal a tussen 0 en 3 en een getal b tussen -2 en 0. Wat is de kans dat het verschil a-b groter is dan 3? 

Uitwerking

De kans gelijk aan ¹/₃

  

Twee gelijkbenige driehoeken

Naar aanleiding van Twee gelijkbenige driehoeken. 't Is dan wel niet echt handig, maar 't kan wel...

\( \eqalign{ & \frac{{BC}} {{\sin 20^\circ }} = \frac{{AC}} {{\sin 80^\circ }} \Rightarrow BC = \frac{{AC \cdot \sin 20^\circ }} {{\sin 80^\circ }} \cr & \frac{{CD}} {{\sin 40^\circ }} = \frac{{AC}} {{\sin 100^\circ }} \Rightarrow CD = \frac{{AC \cdot \sin 40^\circ }} {{\sin 100^\circ }} \cr & BC + CD = \frac{{AC \cdot \sin 20^\circ }} {{\sin 80^\circ }} + \frac{{AC \cdot \sin 40^\circ }} {{\sin 100^\circ }} \cr & BC + CD = \frac{{AC \cdot \sin 20^\circ }} {{\sin 80^\circ }} + \frac{{AC \cdot \sin 40^\circ }} {{\sin 80^\circ }} \cr & BC + CD = \frac{{AC \cdot \sin 20^\circ + AC \cdot \sin 40^\circ }} {{\sin 80^\circ }} \cr & BC + CD = \frac{{AC \cdot \left( {\sin 20^\circ + \sin 40^\circ } \right)}} {{\sin 80^\circ }} \cr & BC + CD = \frac{{AC \cdot \left( {2\sin \frac{{20^\circ + 40^\circ }} {2}\cos \frac{{20^\circ - 40^\circ }} {2}} \right)}} {{\sin 80^\circ }} \cr & BC + CD = \frac{{AC \cdot \left( {2\sin 30^\circ \cos 10^\circ } \right)}} {{\sin 80^\circ }} \cr & BC + CD = \frac{{AC \cdot \cos 10^\circ }} {{\sin 80^\circ }} = AC \cr } \)

Omdat het kan...:-)

De Speld: meer besmettingen door exponentiële groei: kamer eist ingreep in wiskunde

Jos Maalderink en Jop Eikelboom
2 maart 2021, 16:49

Het aantal coronabesmettingen neemt weer gestaag toe, volgens kenners vooral dankzij de exponentiële aard van de verspreiding. De Tweede Kamer eist daarom dat het kabinet ingrijpt in de wiskunde zodat de druk op de samenleving verlicht kan worden.

Geert Wilders (PVV), Kees van der Staaij (SGP) en Pieter Heerma (CDA) in de Tweede Kamer tijdens de schorsing van het debat over de ontwikkelingen rondom het coronavirus.

‘Het aantal nieuwe besmettingen neemt momenteel met 19 procent per week toe. Dat betekent elke vier weken een verdubbeling. Dat is onacceptabel’, zegt CDA-fractievoorzitter Pieter Heerma. ‘Als je de ontwrichting die corona veroorzaakt bij de kern wil aanpakken, moet je bij de wiskunde beginnen. Het kabinet zegt nu: n[t]=n[t-1]*1,19. Als het aan het CDA ligt, is dat voortaan n[t]=n[t-1].’

Ook GroenLinks-leider Jesse Klaver is boos. ‘Het kabinet heeft dit veel te lang op z’n beloop gelaten. Als het kabinet in september al had gekozen voor een negatief lineair verband, had Nederland er nu heel anders voorgestaan. Ik ben geen wiskundige maar volgens mij hadden we dan op dit moment minder dan nul coronapatiënten gehad. Ik vind het heel jammer dat het kabinet die kans heeft laten liggen.’

Forum-leider Thierry Baudet: ‘Wat we nu moeten doen, is de beste differentiaalrekenaars van het land verzamelen en tegen hen zeggen: hoe kunnen we nou de afgeleide van de formule berekenen zodat we weer terug kunnen naar lineaire groei? Maar dat doet het kabinet niet. Rutte en de zijnen blijven maar luisteren naar dezelfde experts die niks anders kunnen dan exponentiële formules plotten. Ik zeg: logaritmes, de Lagrange-multiplicator, floating points enz enz.’

Het aantal delers

'Hoeveel positieve gehele getallen zijn een deler van 5400 of van 18000 (of van allebei)?' 

• Aantal delers

Uitwerking

Er zijn getallen die een deler zijn van 5400 en er zijn getallen die een deler zijn van 18000. Sommige getallen zijn alleen een deler van 5400 en er zijn getallen die alleen een deler zijn van 18000, maar er zijn ook getalen die een deler zijn van 5400 en 18000. De vraag is nu hoe dat zit...👅

Aantal elementen

• Aantal elementen

Steekproeven

Dat vind ik geniaal.

• Welke steekproefgemiddelde kwam het vaakst voor?
• Hoe groot is het gemiddelde van de steekproevenverdeling?
• Geef met de steekproevenverdeling een schatting van het gemiddelde aantal punaises in de doosjes die in deze fabriek worden geproduceerd.

Het antwoord op deze vragen is steeds 204. Dat is een leermoment. Maar ga dat maar 's aan iemand uitleggen...👅

Aantal manieren

Naar aanleiding van aantal manieren: 

In een studentenraad van 16 personen zitten wiskunde- en informaticastudenten, zowel eerste- als ouderejaars. Elke groepering heeft vier vertegenwoordigers in de raad. De studentenraad benoemt een commissie uit haar midden, bestaande uit 6 personen.

1. Op hoeveel manieren is dit mogelijk als er van elke groepering tenminste één vertegenwoordiger in de commissie zitting moet hebben?
2. Op hoeveel manieren is dit mogelijk als er van elke groepering ten hoogste twee vertegenwoordigers in de commissie zitting mogen hebben?

Uitwerking

\( \eqalign{ & a. \cr & \left( {\matrix{ 4 \cr 2 \cr } } \right) \cdot \left( {\matrix{ 4 \cr 1 \cr } } \right)^2 \cdot \left( {\matrix{ 4 \cr 2 \cr } } \right)^2 + \left( {\matrix{ 4 \cr 1 \cr } } \right) \cdot \left( {\matrix{ 4 \cr 1 \cr } } \right)^3 \cdot \left( {\matrix{ 4 \cr 3 \cr } } \right) \cr & b. \cr & \left( {\matrix{ 4 \cr 2 \cr } } \right) \cdot \left( {\matrix{ 4 \cr 1 \cr } } \right)^2 \cdot \left( {\matrix{ 4 \cr 2 \cr } } \right)^2 + \left( {\matrix{ 4 \cr 3 \cr } } \right) \cdot \left( {\matrix{ 4 \cr 2 \cr } } \right)^3 \cdot \left( {\matrix{ 4 \cr 0 \cr } } \right) \cr} \)

Ook mooi...💚

Palindroomgetallen

"Met uitzondering van het getal 11 bestaan alle palindroompriemgetallen uit een oneven aantal cijfers, aangezien de regel voor deelbaarheid door 11 impliceert dat elk palindroomgetal met een even aantal cijfers een veelvoud van 11 is (en dus geen priemgetal). "

• Wikipedia | Palidroomgetal

3456

 \(
\left( {\begin{array}{*{20}c}
   4  \\
   2  \\
\end{array}} \right) \cdot \left( {\begin{array}{*{20}c}
   4  \\
   1  \\
\end{array}} \right)^2  \cdot \left( {\begin{array}{*{20}c}
   4  \\
   2  \\
\end{array}} \right)^2  = 3456
\)