Snijlijn van twee vlakken

In een rechthoekig assenstelsel OXYZ zijn gegeven de punten A(4,0,0), B(4,8,0), C (0,8,0) en T (0,0,8). Op AB ligt punt D(4,6,0).

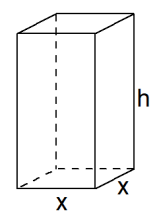
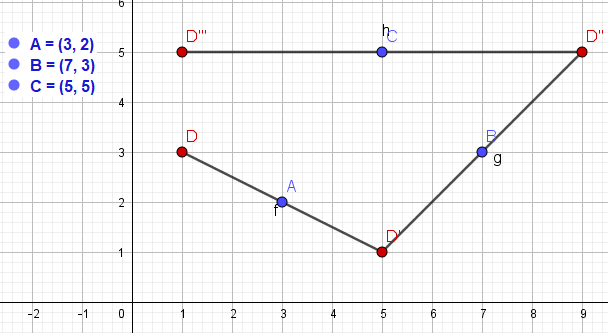
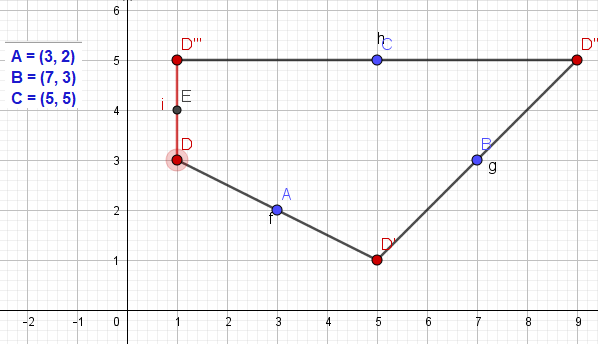
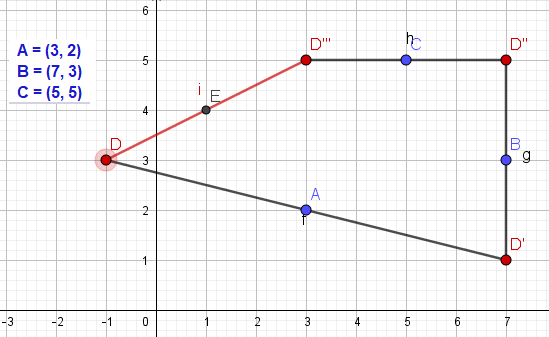
• Bepaal een vectorvoorstelling van de snijlijn van vlak TDO en vlak ACT.

Uitwerking 

$\begin{array}{l} TDO:\lambda \left( {\begin{array}{*{20}c} 2 \\ 3 \\ 0 \\ \end{array}} \right) + \mu \left( {\begin{array}{*{20}c} 0 \\ 0 \\ 1 \\ \end{array}} \right) \\ ACT:\left( {\begin{array}{*{20}c} 4 \\ 0 \\ 0 \\ \end{array}} \right) + \rho \left( {\begin{array}{*{20}c} { - 1} \\ 2 \\ 0 \\ \end{array}} \right) + \tau \left( {\begin{array}{*{20}c} { - 1} \\ 0 \\ 2 \\ \end{array}} \right) \\ \left\{ \begin{array}{l} 2\lambda = 4 - \rho - \tau \\ 3\lambda = 2\rho \\ \mu = 2\tau \\ \end{array} \right. \\ \left\{ \begin{array}{l} 4\lambda = 8 - 2\rho - 2\tau \\ 3\lambda = 2\rho \\ \mu = 2\tau \\ \end{array} \right. \\ \left\{ \begin{array}{l} 4\lambda = 8 - 3\lambda - \mu \\ 3\lambda = 2\rho \\ \mu = 2\tau \\ \end{array} \right. \\ \mu = - 7\lambda + 8 \\ l:\lambda \left( {\begin{array}{*{20}c} 2 \\ 3 \\ 0 \\ \end{array}} \right) + \left( { - 7\lambda + 8} \right)\left( {\begin{array}{*{20}c} 0 \\ 0 \\ 1 \\ \end{array}} \right) \\ l:\lambda \left( {\begin{array}{*{20}c} 2 \\ 3 \\ 0 \\ \end{array}} \right) + - 7\lambda \cdot \left( {\begin{array}{*{20}c} 0 \\ 0 \\ 1 \\ \end{array}} \right) + 8 \cdot \left( {\begin{array}{*{20}c} 0 \\ 0 \\ 1 \\ \end{array}} \right) \\ l:\left( {\begin{array}{*{20}c} 0 \\ 0 \\ 8 \\ \end{array}} \right) + \lambda \left( {\begin{array}{*{20}c} 2 \\ 3 \\ { - 7} \\ \end{array}} \right) \\ \end{array}$

---

• Examenvraag 82-83 (4)

Geneste wortel

$\begin{array}{l} \sqrt {2 - \sqrt 3 } = \sqrt a - \sqrt b \\ 2 - \sqrt 3 = a - 2\sqrt {ab} + b \\ \left\{ \begin{array}{l} a + b = 2 \\ 2\sqrt {ab} = \sqrt 3 \\ \end{array} \right. \\ \left\{ \begin{array}{l} a + b = 2 \\ 4ab = 3 \\ \end{array} \right. \\ \left\{ \begin{array}{l} a = 1\frac{1}{2} \\ b = \frac{1}{2} \\ \end{array} \right. \\ \sqrt {2 - \sqrt 3 } = \sqrt {1\frac{1}{2}} - \sqrt {\frac{1}{2}} \\ \sqrt {2 - \sqrt 3 } = \frac{1}{2}\sqrt 6 - \frac{1}{2}\sqrt 2 \\ \end{array}$

Zelf doen

• Verzin er zelf maar een vraag bij...:-)

Vraag 10

Een fabrikant van pralines verpakt reeds jaren zijn leveringen aan grootwarenhuizen in dozen met een vierkante grondoppervlakte (zijde is 8 cm) en een hoogte van 21 cm. Hij zou graag de inhoud van zijn dozen vergroten maar wil niet meer betalen aan karton voor zijn dozen.

• Wat zijn de afmetingen van de zijden van het grondvlak en de hoogte waarbij de inhoud maximaal wordt?

Uitwerkingen

Eerst maar 's een tekening:

1. De totale oppervlakte bestaat uit 4 zijvlakken van 8x21, een grondvlak van 8² en een bovenvlak van 8². Meer in 't algemeen: je hebt 4 zijvlakken van hx, een grondvlak van x2 en een bovenvlak van x2. Optellen en je hebt je formule voor de oppervlakte O. Invullen van x=8 en h=21 zal dan wel lukken.
2. Als je een formuie hebt met O=...·xh+...·x2 en je weet dat O de oppervlakte van het pak is als x=8 en h=21 dan kan je de formule herschrijven waarbij je h uitdrukt in x.
3. De inhoud van de balk is gelijk aan I=x2·h. Vul voor h de formule in die je bij b. gevonden hebt. Je krijgt dan een formule voor de inhoud I uitgedrukt in x.
4. Bepaal de afgeleide van de functie die je bij c. gevonden hebt.
5. Stel de afgeleide nul, los op en je hebt mogelijke kandidaten voor x waarbij je grootste inhoud hebt.
6. Als je de waarde van x gevonden hebt dan kan je de bijbehorende waarde van h uitrekenen. Wat valt je op?

Twee voorbeelden van eenvoudige vlakvullingen

Eén eenvoudige manier om een vlakvulling te maken is uitgaan van (bijvoorbeeld) een gelijkzijdige driehoek en te zorgen dat je tekening aansluit... dus A en A', B en B' en C aan C'.



Dat geeft dan als vlakvulling:



Vierkant
Dat kan uit als je uitgaat van een vierkant:



Dat geeft dan:



Dat is dan toch wel aardig toch?

Veelhoeken en middens van zijden - deel 2

Je kunt bij een gegeven aantal oneven middens een n-hoek tekenen. Dat lukt altijd. Bij een willekeurig startpunt kan je het 'beoogde startpunt' vinden op het midden van start- en eindpunt.



Eigenlijk had D''' op D uit moeten komen. Om het te laten kloppen moet je D kiezen op het midden van DD''':



Dus kies D op E.



Mission accomplised.

Je kunt overigens bij gegeven middens het startpunt ook berekenen: Dit doe je door het om en om optellen en aftrekken van de coördinaten van de middens te nemen.

x:=2-5+3=0
y:=1-3+4=2

Neem D(0,2).

Dat werkt bij oneven aantallen. Voor even aantallen gelden weer andere dingen.

Veelhoeken en middens van zijden

Neem 's aan dat je bij een gegeven n punten een n-hoek moet tekenen waarvan die punten de middens zijn van de zijden. Dus (bijvoorbeeld) zoiets als:



Je kunt er dan achter komen dat dit met 4 willekeurige punten (of elk even aantal) niet altijd gaat lukken. Na 3 punten ligt het 4e punt in feite al vast.



Het 4e midden moet op de zijde in het midden van DD''' liggen. Daarmee krijg je een vierhoek die klopt.



Nu kun je punt D verplaatsen en kan je voor D elke willekeurig lokatie kiezen.



Voor oneven n geldt dat niet. Daar is ook van alles te beleven...

Verschillende soorten symmetrie

Draaisymmetrie	Puntsymmetrie	Schuifsymmetrie
Draaisymmetrie, maar dan moet je niet op kleur letten.	Puntsymmetrie als je niet op de kleur let.	Je kunt de figuren naar rechts (of naar links) verschuiven.
Lijnsymmetrie	Puntsymmetrie	Draaisymmetrie
De rode lijn geeft aan dat de figuren lijnsymmetrisch zijn.	De katten zijn puntsymmetrisch t.o.v. de groene punt.	De groen punt is het centrum van draaiing over 120°. Er zijn natuurlijk nog veel meer punten te vinden.

De snijlijn van twee vlakken

Gegeven:

$\begin{array}{l}  V:x - y + z = 4 \\  W:3x - 2y - z = 5 \\  \end{array}$

Gevraagd:

• Geef een vectorvoorstelling van de snijlijn van V en W.

Uitwerking:

Maak een stelsel van twee vergelijkingen:

$\left\{ \begin{array}{l}  x - y + z = 4 \\  3x - 2y - z = 5 \\  \end{array} \right.$

Als je zorgt dat er een variabel weg valt kan je vervolgens met dit stelsel de vergelijking vinden van een derde vlak waarin de snijlijn ligt:

$\begin{array}{l}  \left\{ \begin{array}{l}  x - y + z = 4 \\  3x - 2y - z = 5 \\  \end{array} \right. \\  (1) + (2) \\  x - y + 3x - 2y = 9 \\  4x - 3y = 9 \\  \end{array}$

Ik kan nu x, y en z uitdrukken in $\lambda$ en mijn vectorvoorstelling opstellen:

$\begin{array}{l}  Kies\,\,y = \lambda  \\  4x - 3\lambda  = 9 \\  4x = 3\lambda  + 9 \\  x = \frac{3}{4}\lambda  + 2\frac{1}{4} \\  \frac{3}{4}\lambda  + 2\frac{1}{4} - \lambda  + z = 4 \\  z = \frac{1}{4}\lambda  + 1\frac{3}{4} \\  \left( {\begin{array}{*{20}c}    x  \\    y  \\    z  \\ \end{array}} \right) = \left( {\begin{array}{*{20}c}    {2\frac{1}{4}}  \\    0  \\    {1\frac{3}{4}}  \\ \end{array}} \right) + \lambda \left( {\begin{array}{*{20}c}    {\frac{3}{4}}  \\    1  \\    {\frac{1}{4}}  \\ \end{array}} \right) \\  \left( {\begin{array}{*{20}c}    x  \\    y  \\    z  \\ \end{array}} \right) = \left( {\begin{array}{*{20}c}    {2\frac{1}{4}}  \\    0  \\    {1\frac{3}{4}}  \\ \end{array}} \right) + \lambda \left( {\begin{array}{*{20}c}    3  \\    4  \\    1  \\ \end{array}} \right) \\  \end{array}$

Zie zo...:-)

Hoeken berekenen in een regelmatige vierzijdige piramide

Teken een regelmatige vierzijdige piramide T ABCD met hoogte 4 en ribbe grondvlak 4, xas//AD en y as//AB. Neem als oorsprong het snijpunt AC en BD. P is het midden van AT.

1. Bereken de hoek van DP en de vlakken ACT en BDT.
2. Bereken de hoek van de vlakken ABT en ADT.

---

• Hoeken berekenen in een regelmatige 4-zijdige piramide

Afstand van punt en lijn

Teken een kubus ABCO·DEFG met de x as langs OA, de y as langs OC en de z as langs OG. De ribbe van de kubus is 2. Als P het midden is van ribbe FG en Q het midden van ribbe BC.

• Bereken dan de afstand van het punt P tot de lijn AQ.

Uitwerking



Eerst maar 's een vectorvoorstelling van de lijn AQ:

$AQ:\left( {\begin{array}{*{20}c}    x  \\    y  \\    z  \\ \end{array}} \right) = \left( {\begin{array}{*{20}c}    2  \\    0  \\    0  \\ \end{array}} \right) + \lambda \left( {\begin{array}{*{20}c}    { - 1}  \\    2  \\    0  \\ \end{array}} \right)$

Neem dan het vlak V loodrecht op AQ en waar P in ligt:

$\begin{array}{l}  V: - x + 2y = d \\  P(0,1,2)\,\,\,in\,\,\,V \\  d = 2 \\  \end{array}$

Je kunt V snijden met AQ om P' te vinden:

$\begin{array}{l}  V: - x + 2y = 2 \\   - \left( {2 - \lambda } \right) + 2\left( {2\lambda } \right) = 2 \\   - 2 + \lambda  + 4\lambda  = 2 \\  5\lambda  = 4 \\  \lambda  = \frac{4}{5} \\  P'\left( {1\frac{1}{5},1\frac{3}{5},0} \right) \\  \end{array}$

En dan zijn we er wel zo'n beetje:

$d(PP') = \sqrt {\left( {1\frac{1}{5} - 0} \right)^2  + \left( {1\frac{3}{5} - 1} \right)^2  + \left( {0 - 2} \right)^2 }  = \frac{1}{5}\sqrt {145}$

Dat kan ook...:-)

---

• Re: Afstand punt tot lijn in een kubus 

---