Vraag 10

Een fabrikant van pralines verpakt reeds jaren zijn leveringen aan grootwarenhuizen in dozen met een vierkante grondoppervlakte (zijde is 8 cm) en een hoogte van 21 cm. Hij zou graag de inhoud van zijn dozen vergroten maar wil niet meer betalen aan karton voor zijn dozen.

• Wat zijn de afmetingen van de zijden van het grondvlak en de hoogte waarbij de inhoud maximaal wordt?

Uitwerkingen

Eerst maar 's een tekening:

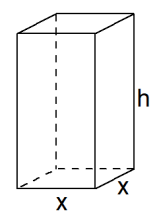
1. De totale oppervlakte bestaat uit 4 zijvlakken van 8x21, een grondvlak van 8² en een bovenvlak van 8². Meer in 't algemeen: je hebt 4 zijvlakken van hx, een grondvlak van x2 en een bovenvlak van x2. Optellen en je hebt je formule voor de oppervlakte O. Invullen van x=8 en h=21 zal dan wel lukken.
2. Als je een formuie hebt met O=...·xh+...·x2 en je weet dat O de oppervlakte van het pak is als x=8 en h=21 dan kan je de formule herschrijven waarbij je h uitdrukt in x.
3. De inhoud van de balk is gelijk aan I=x2·h. Vul voor h de formule in die je bij b. gevonden hebt. Je krijgt dan een formule voor de inhoud I uitgedrukt in x.
4. Bepaal de afgeleide van de functie die je bij c. gevonden hebt.
5. Stel de afgeleide nul, los op en je hebt mogelijke kandidaten voor x waarbij je grootste inhoud hebt.
6. Als je de waarde van x gevonden hebt dan kan je de bijbehorende waarde van h uitrekenen. Wat valt je op?