"Op een wikkel van een suikerklontje staat op zes verschillende plaatsen in zes verschillende talen het woord suiker. Er wordt gekozen uit tien talen waaronder Nederlands. Hoeveel verschillende wikkels zijn er mogelijk waarop je het woord 'suiker' aantreft?"
Uitgewerkt:-)
\( \left( {10} \right)_6 - \left( 9 \right)_6 = {\rm{151}}{\rm{.200 - 60}}{\rm{.480 = 90}}{\rm{.720}} \)
Dataset
Eén 6 als kleinste getal.
Dan 26 keer een willekeurig getal tussen 6 en 8,1.
Een 8,1 voor de mediaan.
Dan 26 keer een willekeuirg getal tussen 8,1 en 9.
En tenslotte één 9 als grootste getal.
Boxplot
Nog meer verhoudingen bij Lengte ribben berekenen. Hoe pak je zoiets aan? 't Is een monster...
\( \eqalign{ & a:b:c = 4(a + b + c):2(ab + ac + bc):abc \cr & I. \cr & a:c = 4(a + b + c):abc \cr & c = \frac{{a^2 b - 4a - 4b}} {4} \cr & II. \cr & b:c = 2(ab + ac + bc):abc \cr & c = \frac{{ab(b - 2)}} {{2(a + b)}} \cr & Geeft: \cr & \frac{{a^2 b - 4a - 4b}} {4} = \frac{{ab(b - 2)}} {{2(a + b)}} \cr & a^2 b - 4a - 4b = \frac{{2ab(b - 2)}} {{a + b}} \cr & (a^2 b - 4a - 4b)(a + b) = 2ab(b - 2) \cr & a^3 b - 4a^2 - 4ab + a^2 b^2 - 4b^2 - 2ab^2 = 0 \cr & \left( {a^2 - 2a - 4} \right)b^2 + \left( {a^3 - 4a} \right)b - 4a^2 = 0 \cr & b^2 + \frac{{a^3 - 4a}} {{a^2 - 2a - 4}}b - \frac{{4a^2 }} {{a^2 - 2a - 4}} = 0 \cr & \left( {b + \frac{{a^3 - 4a}} {{2a^2 - 4a - 8}}} \right)^2 - \left( {\frac{{a^3 - 4a}} {{a^2 - 2a - 4}}} \right)^2 - \frac{{4a^2 }} {{a^2 - 2a - 4}} = 0 \cr & \left( {b + \frac{{a^3 - 4a}} {{2a^2 - 4a - 8}}} \right)^2 - \frac{{a^6 - 4a^4 - 8a^3 }} {{\left( {a^2 - 2a - 4} \right)^2 }} = 0 \cr & b = - \frac{{a^3 - 4a}} {{2a^2 - 4a - 8}} \pm \sqrt {\frac{{a^6 - 4a^4 - 8a^3 }} {{\left( {a^2 - 2a - 4} \right)^2 }}} \cr} \)
Bij zo'n vraag als De lengte van ribben van een balk berekenen is het altijd even de vraag hoe je verhoudingen kunt vertalen naar vergelijkingen. Vergelijkingen kan je in een stelsel van vergelijkingen zetten en fijn oplossen. Of nog beter: laat ze oplossen...😀
In het geval van bovenstand probleem zou dat zo kunnen:
\( \begin{array}{l} ab:ac:bc = 1:5:10 \\ \frac{{ab}}{{ac}} = \frac{1}{5} \Rightarrow \frac{b}{c} = \frac{1}{5} \Rightarrow 5b = c \\ \frac{{ab}}{{bc}} = \frac{1}{{10}} \Rightarrow \frac{a}{c} = \frac{1}{{10}} \Rightarrow 10a = c \\ \left\{ \begin{array}{l} abc = 160 \\ 5b = c \\ 10a = c \\ \end{array} \right. \Rightarrow \left\{ \begin{array}{l} a = 2 \\ b = 4 \\ c = 20 \\ \end{array} \right. \\ \end{array} \)
Uitgewerkt:
\( \begin{array}{l} \left\{ \begin{array}{l} abc = 160 \\ b = \frac{1}{5}c \\ a = \frac{1}{{10}}c \\ \end{array} \right. \Rightarrow \\ \frac{1}{{10}}c \cdot \frac{1}{5}c \cdot c = 160 \\ \frac{1}{{50}}c^3 = 160 \\ c^3 = 8000 \\ c = 20 \\ \left\{ \begin{array}{l} a = 2 \\ b = 4 \\ c = 20 \\ \end{array} \right. \\ \end{array} \)Als je dat kan dan kan je Lengte ribben berekenen ook 's proberen...👅
Naar aanleiding van Hoe bereken je de hoek tussen de wijzers van de klok?
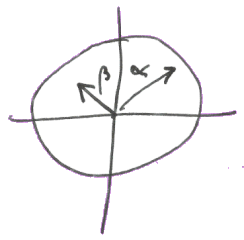
\( \eqalign{ & y:x\,\,\,uur \cr & \alpha = 6x \cr & \beta = 360 - \frac{1} {2}\left( {60y + x} \right) \cr & \alpha = \beta \cr & 6x = 360 - \frac{1} {2}\left( {60y + x} \right) \cr & 6x = 360 - 30y - \frac{1} {2}x \cr & 6\frac{1} {2}x = 360 - 30y \cr & 13x = 720 - 60y \cr & x = \frac{{720 - 60y}} {{13}} \cr} \)
Enz...👅
Soms levert een antwoord in WisFaq van allerlei ideetjes op. Dit is wel een geschikt probleem voor probleemaanpak. Je kunt zelfs randomizeren met de uren. In het voorbeeld ging het om een tijd tussen 10 en 11, maar je kan natuurlijk ook bij andere tijden kijken.
Je weet maar nooit wanneer dat weer 's van pas komt. Om maar 's wat te noemen, qua opbrengsten. Voor de rest moet ik er nog maar 's over nadenken... over het conceptueel strategisch beleidsplan, zullen we maar zeggen...
Inhoudsopgave
Lesbrieven
Inhoudsopgave
Lesbrieven
Inhoudsopgave
Lesbrieven
Inhoudsopgave
Lesbrieven