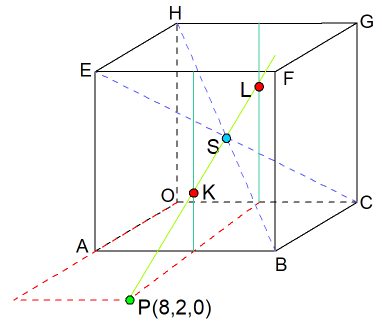
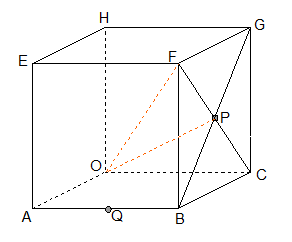
De x-as langs OA, de y-as langs OC en de z-as langs OT.
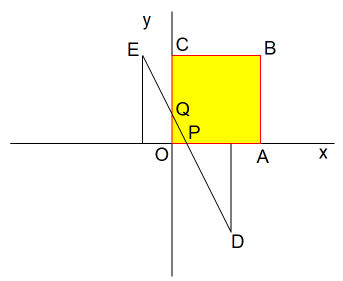
Door de punten D(2,-3,2) en E (-1,3,0) trekt men een lijn die de piramide snijdt in de punten P en Q.
- Maak een duidelijke tekening en bereken |PQ|.
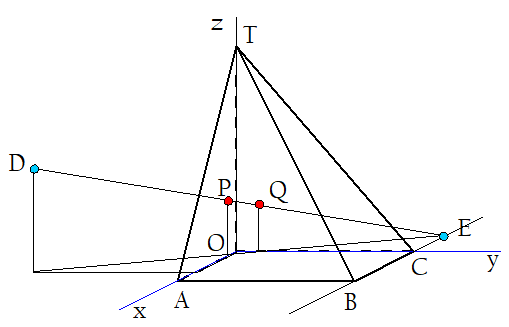
Dat is alvast een goed begin... het halve werk... later misschien meer...:-)
Maar als je twijfelt kan je altijd een bovenaanzicht tekenen en dan kijken of je een beetje in de goede richting zit.
\( \begin{array}{l} {\rm{Gegeven:}} \\ {\rm{D(2}}{\rm{, - 3}}{\rm{,2)\,\,en\,\,E ( - 1}}{\rm{,3}}{\rm{,0)}} \\ \overrightarrow {DE} = \left( {\begin{array}{*{20}c} 2 \\ { - 3} \\ 2 \\ \end{array}} \right) + \lambda \left( {\begin{array}{*{20}c} 3 \\ { - 6} \\ 2 \\ \end{array}} \right) \\ Vlak\,\,\,OAT:y = 0 \\ - 3 + - 6\lambda = 0 \\ 6\lambda = - 3 \\ \lambda = - \frac{1}{2} \\ \left\{ \begin{array}{l} x = 2 + 3 \cdot - \frac{1}{2} = \frac{1}{2} \\ y = 0 \\ z = 2 + 2 \cdot - \frac{1}{2} = 1 \\ \end{array} \right. \Rightarrow P\left( {\frac{1}{2},0,1} \right) \\ Vlak\,\,\,OCT:x = 0 \\ 2 + 3\lambda = 0 \\ 3\lambda = - 2 \\ \lambda = - \frac{2}{3} \\ \left\{ \begin{array}{l} x = 0 \\ y = - 3 - 6 \cdot - \frac{2}{3} = 1 \\ z = 2 + 2 \cdot - \frac{2}{3} = \frac{2}{3} \\ \end{array} \right. \Rightarrow Q\left( {0,1,\frac{2}{3}} \right) \\ P\left( {\frac{1}{2},0,1} \right)\,\,\,en\,\,\,Q\left( {0,1,\frac{2}{3}} \right) \\ d(P,Q) = \sqrt {\left( {\frac{1}{2}} \right)^2 + \left( { - 1} \right)^2 + \left( {1 - \frac{2}{3}} \right)^2 } \\ d(P,Q) = \sqrt {\frac{1}{4} + 1 + \frac{1}{9}} = 1\frac{1}{6} \\ \end{array} \)