't Kwam vandaag nog even ter sprake.., transformaties van grafieken... waarbij iedereen mij altijd zo glazig zat aan te kijken... nu op papier...:-)
vrijdag 14 december 2018
Tranformaties van grafieken
't Kwam vandaag nog even ter sprake.., transformaties van grafieken... waarbij iedereen mij altijd zo glazig zat aan te kijken... nu op papier...:-)
zondag 25 november 2018
zondag 11 november 2018
zaterdag 10 november 2018
Opgelost...:-)
SOLVE([2·s + 2·s + 2·s = 30, h + h + 2·s = 20, 2·f + 2·f + h = 13], [f, h, s])
[f = 2 h = 5 s = 5]
f := 2
h := 5
s := 5
s + h*f
15
Opgelost...:-)
vrijdag 9 november 2018
Proof en pudding
\(
\eqalign{
& \frac{{\cos \left( u \right) + \sin \left( u \right)}}
{{\cos \left( u \right) - \sin \left( u \right)}} = \frac{{1 + \sin (2u)}}
{{\cos (2u)}} \cr
& \frac{{\left( {\cos \left( u \right) + \sin \left( u \right)} \right)\left( {\cos \left( u \right) - \sin \left( u \right)} \right)}}
{{\left( {\cos \left( u \right) - \sin \left( u \right)} \right)^2 }} = \frac{{1 + \sin (2u)}}
{{\cos (2u)}} \cr
& \frac{{\cos ^2 \left( u \right) - \sin ^2 \left( u \right)}}
{{\cos ^2 (u) - 2\sin (u)\cos (u) + \sin ^2 (u)}} = \frac{{1 + \sin (2u)}}
{{\cos (2u)}} \cr
& \frac{{\cos \left( {2u} \right)}}
{{1 - \sin (2u)}} = \frac{{1 + \sin (2u)}}
{{\cos (2u)}} \cr
& \cos ^2 (2u) = 1 - \sin ^2 (2u) \cr
& \sin ^2 (2u) + \cos ^2 (2u) = 1 \cr
& {\text{Klopt!}} \cr}
\)
maandag 8 oktober 2018
Programmeren voor dummies (2)
function kapIPv6(ip)
dim s
iF ip<>"" AND InStr(ip,":")>0 Then
s=Replace(ip,":","|",1,3)
s=Left(s,Instr(s,":")-1)
s=Replace(s,"|",":",1,3)
kapIPv6=s
else
kapIPv6=""
end if
end function
dim s
iF ip<>"" AND InStr(ip,":")>0 Then
s=Replace(ip,":","|",1,3)
s=Left(s,Instr(s,":")-1)
s=Replace(s,"|",":",1,3)
kapIPv6=s
else
kapIPv6=""
end if
end function
zondag 7 oktober 2018
Programmeren voor dummies
Function RemoveNumber(s)
s=replace(s,"0. ","")
s=replace(s,"1. ","")
s=replace(s,"2. ","")
s=replace(s,"3. ","")
s=replace(s,"4. ","")
s=replace(s,"5. ","")
s=replace(s,"6. ","")
s=replace(s,"7. ","")
s=replace(s,"8. ","")
s=replace(s,"9. ","")
s=replace(s,"A. ","")
s=replace(s,"B. ","")
s=replace(s,"C. ","")
s=replace(s,"D. ","")
s=replace(s,"E. ","")
s=replace(s,"F. ","")
s=replace(s,"G. ","")
s=replace(s,"H. ","")
s=replace(s,"I. ","")
s=replace(s,"J. ","")
s=replace(s,"K. ","")
s=replace(s,"L. ","")
s=replace(s,"M. ","")
s=replace(s,"N. ","")
s=replace(s,"O. ","")
s=replace(s,"P. ","")
s=replace(s,"Q. ","")
s=replace(s,"R. ","")
s=replace(s,"S. ","")
s=replace(s,"T. ","")
s=replace(s,"U. ","")
s=replace(s,"V. ","")
s=replace(s,"W. ","")
s=replace(s,"X. ","")
s=replace(s,"Y. ","")
s=replace(s,"Z. ","")
RemoveNumber=s
End Function
s=replace(s,"0. ","")
s=replace(s,"1. ","")
s=replace(s,"2. ","")
s=replace(s,"3. ","")
s=replace(s,"4. ","")
s=replace(s,"5. ","")
s=replace(s,"6. ","")
s=replace(s,"7. ","")
s=replace(s,"8. ","")
s=replace(s,"9. ","")
s=replace(s,"A. ","")
s=replace(s,"B. ","")
s=replace(s,"C. ","")
s=replace(s,"D. ","")
s=replace(s,"E. ","")
s=replace(s,"F. ","")
s=replace(s,"G. ","")
s=replace(s,"H. ","")
s=replace(s,"I. ","")
s=replace(s,"J. ","")
s=replace(s,"K. ","")
s=replace(s,"L. ","")
s=replace(s,"M. ","")
s=replace(s,"N. ","")
s=replace(s,"O. ","")
s=replace(s,"P. ","")
s=replace(s,"Q. ","")
s=replace(s,"R. ","")
s=replace(s,"S. ","")
s=replace(s,"T. ","")
s=replace(s,"U. ","")
s=replace(s,"V. ","")
s=replace(s,"W. ","")
s=replace(s,"X. ","")
s=replace(s,"Y. ","")
s=replace(s,"Z. ","")
RemoveNumber=s
End Function
woensdag 3 oktober 2018
donderdag 27 september 2018
Bezemklas
In het kader van hulp voor wiskunde en het achterstallig onderhoud.
Opzet en werkwijze
Samenvatting en checklists voor SE1
Rooster voor hulp
Handige hulpjes
Opzet en werkwijze
- Voorbereiden op je SE.
- Extra uitleg en praktische tips.
- Vragen stellen.
- Samen opgaven en examenopgaven maken.
- Examentraining.
- Individuele bijles of in kleine groepjes (maximaal 4 leerlingen).
- Samenvattingen, uitwerkingen en checklists.
- Oefenen in de digitale wiskundeomgeving.
- Online ondersteuning.
Samenvatting en checklists voor SE1
Rooster voor hulp
Handige hulpjes
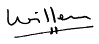
zondag 16 september 2018
vrijdag 14 september 2018
Klas 3
Het was enigszins een verrassing maar we gebruiken in de derde klas dit jaar nog even Getal en Ruimte. De samenvattingen en checklists op wiskundeleraar kunnen dus nog een jaartje mee. Dat is dan wel weer aardig...:-)

Dat is dan gratis maar niet voor niets...:-)

Dat is dan gratis maar niet voor niets...:-)
zondag 9 september 2018
HAVO wiskunde B

- formules, grafieken en vergelijkingen
- veranderingen
- hoeken en afstanden
- werken met formules
- machten, exponenten en logaritmen
- de afgeleide functie
- lijnen en cirkels
- goniometrie
- exponentiële verbanden
- meetkundige berekeningen
- verbanden en functies
- examentraining
HAVO wiskunde A


- rekenregels en verhoudingen
- verwerken van data
- tabellen en grafieken
- handig tellen
- lineaire verbanden
- statistiek en beslissingen
- statistiek met de computer
- veranderingen
- exponentiële verbanden
- statistische variabelen
- formules en vergelijkingen
- examentraining
zaterdag 8 september 2018
Lerarentekort
Je ziet het gebeuren... Wij willen geen coach zijn wij zijn leraren... toch doen... wij willen geen groepen van 60-90... maar toch doen... Maar we willen ook geen #lerarentekort - in dat geval... maak een keus... zo niet... ga dan iets nuttigs doen... vuilnis ophalen of zo....:-)
vrijdag 7 september 2018
Week 36
 Voor school heb ik inmiddels NumWorks klaar gezet voor 4 en 5 HAVO wiskunde A en B. Dat was nog een werkje. Hoe deed ik dat ook alweer? Maar dat is inmiddels wel gelukt. Volgens mij gaan we de instroommodules doen zoals ik die vorig jaar van plan was. Dat is mooi. Voor de rest van de dingen moeten we nog overleggen. Ik heb voor mijn collega's inmiddels ook de toetsen van 2016-2017 en 2017-2018 verzameld. Dat kan ze nog richting geven... en mogelijk een hoop werk besparen.
Voor school heb ik inmiddels NumWorks klaar gezet voor 4 en 5 HAVO wiskunde A en B. Dat was nog een werkje. Hoe deed ik dat ook alweer? Maar dat is inmiddels wel gelukt. Volgens mij gaan we de instroommodules doen zoals ik die vorig jaar van plan was. Dat is mooi. Voor de rest van de dingen moeten we nog overleggen. Ik heb voor mijn collega's inmiddels ook de toetsen van 2016-2017 en 2017-2018 verzameld. Dat kan ze nog richting geven... en mogelijk een hoop werk besparen.'t Weekend staat voor de deur... dus vandaag doen we rustig aan.:-)
Numworks docenten
maandag 30 juli 2018
zaterdag 28 juli 2018
Nikolay Bogdanov-Belsky
In 1895, Nikolay Bogdanov-Belsky painted the famous: "Mental Arithmetic.
In the Public School of S. Rachinsky." The problem on the blackboard is
(10²+11²+12²+13²+14²)/365, can you find a way to solve it with mental
arithmetic?
\( \eqalign{ & \frac{{10^2 + 11^2 + 12^2 + 13^2 + 14^2 }} {{365}} = \cr & \frac{{10^2 + \left( {10 + 1} \right)^2 + (10 + 2)^2 + (10 + 3)^2 + (10 + 4)^2 }} {{365}} = \cr & \frac{{5 \cdot 10^2 + 2 \cdot 10 + 4 \cdot 10 + 6 \cdot 10 + 8 \cdot 10 + 1 + 4 + 9 + 16}} {{365}} = \cr & \frac{{500 + 200 + 30}} {{365}} = \cr & \frac{{730}} {{365}} = 2 \cr} \)
\( \eqalign{ & \frac{{10^2 + 11^2 + 12^2 + 13^2 + 14^2 }} {{365}} = \cr & \frac{{10^2 + \left( {10 + 1} \right)^2 + (10 + 2)^2 + (10 + 3)^2 + (10 + 4)^2 }} {{365}} = \cr & \frac{{5 \cdot 10^2 + 2 \cdot 10 + 4 \cdot 10 + 6 \cdot 10 + 8 \cdot 10 + 1 + 4 + 9 + 16}} {{365}} = \cr & \frac{{500 + 200 + 30}} {{365}} = \cr & \frac{{730}} {{365}} = 2 \cr} \)
woensdag 18 juli 2018
Week 34
This is the end...
Met ingang van 18-7-2018 stop ik definitief met de weekpuzzels. 't Was leuk maar de koek is op...:-)
zondag 15 juli 2018
Week 32
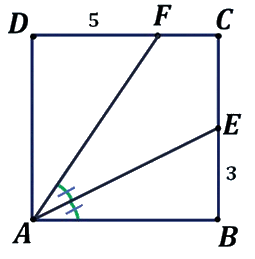
ABCD is een vierkant met AE de deellijn van de hoek BAF.
- Bereken de lengte van AF.
woensdag 27 juni 2018
Week 31
Iemand heeft een rechthoekig stuk zink, 80 cm breed. Hij wil daarvan een goot maken met rechthoekige doorsnede.


- Ga na, wanneer de goot een zo groot mogelijke doorsnede heeft.
donderdag 21 juni 2018
dinsdag 19 juni 2018
maandag 18 juni 2018
Ook leuk:-)
Het berekenen van de snijpunten:
\(
\eqalign{
& \cos (x) = \cos (2x - 1) \cr
& x = 2x - 1 + k \cdot 2\pi \vee x = - (2x - 1) + k \cdot 2\pi \cr
& - x = - 1 + k \cdot 2\pi \vee x = - 2x + 1 + k \cdot 2\pi \cr
& x = 1 + k \cdot 2\pi \vee 3x = 1 + k \cdot 2\pi \cr
& x = 1 + k \cdot 2\pi \vee x = \frac{1}
{3} + k \cdot \frac{2}
{3}\pi \cr}
\)
Dat zou zo maar kunnen...:-)
zaterdag 16 juni 2018
Grafieken en zo...
Maar wat is wat?
\( \eqalign{ & f(x) = (x - 2)^3 - 3 \cr & g(x) = f\left( {\frac{1} {2}x + 2} \right) \cr & h(x) = g(x) - f(x) \cr & i(x) = h'(x) \cr} \)
Om maar 's wat te noemen...:-)
zaterdag 2 juni 2018
In de driehoek van Pascal
In de driehoek van Pascal:
\( \begin{array}{l} \left( {\begin{array}{*{20}c} n \\ k \\ \end{array}} \right) + 2 \cdot \left( {\begin{array}{*{20}c} n \\ {k - 1} \\ \end{array}} \right) + \left( {\begin{array}{*{20}c} n \\ {k - 2} \\ \end{array}} \right) = \\ \left( {\begin{array}{*{20}c} n \\ {k - 2} \\ \end{array}} \right) + \left( {\begin{array}{*{20}c} n \\ {k - 1} \\ \end{array}} \right) + \left( {\begin{array}{*{20}c} n \\ {k - 1} \\ \end{array}} \right) + \left( {\begin{array}{*{20}c} n \\ k \\ \end{array}} \right) = \\ \left( {\begin{array}{*{20}c} {n + 1} \\ {k - 1} \\ \end{array}} \right) + \left( {\begin{array}{*{20}c} {n + 1} \\ k \\ \end{array}} \right) = \\ \left( {\begin{array}{*{20}c} {n + 2} \\ k \\ \end{array}} \right) \\ \end{array} \)
\( \begin{array}{l} \left( {\begin{array}{*{20}c} n \\ k \\ \end{array}} \right) + 2 \cdot \left( {\begin{array}{*{20}c} n \\ {k - 1} \\ \end{array}} \right) + \left( {\begin{array}{*{20}c} n \\ {k - 2} \\ \end{array}} \right) = \\ \left( {\begin{array}{*{20}c} n \\ {k - 2} \\ \end{array}} \right) + \left( {\begin{array}{*{20}c} n \\ {k - 1} \\ \end{array}} \right) + \left( {\begin{array}{*{20}c} n \\ {k - 1} \\ \end{array}} \right) + \left( {\begin{array}{*{20}c} n \\ k \\ \end{array}} \right) = \\ \left( {\begin{array}{*{20}c} {n + 1} \\ {k - 1} \\ \end{array}} \right) + \left( {\begin{array}{*{20}c} {n + 1} \\ k \\ \end{array}} \right) = \\ \left( {\begin{array}{*{20}c} {n + 2} \\ k \\ \end{array}} \right) \\ \end{array} \)
dinsdag 29 mei 2018
zaterdag 26 mei 2018
maandag 21 mei 2018
WisFaq
zaterdag 19 mei 2018
Aansluiting hoger onderwijs
Een aantal jaren geleden was er in het kader van aansluitproblemen toch
wel een soort notie wat er zou moeten gebeuren. In het verslag van de
bijeenkomst VO-HO aansluiting wiskunde 23 april 2007 kwam ik een
'wensenlijstje'
tegen met ‘wat studenten wiskunde zouden moeten beheersen’:
- redeneren
- notaties kunnen lezen en schrijven
- gevoel voor abstractie
- een bepaalde werk- en studiehouding
donderdag 17 mei 2018
De examensyllabi
"Volgens LAKS hadden leerlingen veel onduidelijkheid voor zichzelf kunnen voorkomen door de examensyllabi vooraf goed te lezen."
bron
- eh... dat is een docententaak en leg het een 't ander uit misschien?:-)
Of... zet het op je website...:-) wiskundeleraar.nl/page3ict.asp?n… #wiskundeB #HAVO - kan nog net....:-)
Of nog mooier expliciteer alles wat leerlingen moeten kennen, kunnen en begrijpen... #begripeninzicht zie bijvoorbeeld wiskundeleraar.nl/paGe3ict.asp?n…
Zie ook wiskundeleraar.nl/paGe3ict.asp?n… voor HAVO wiskunde A
...ook buitengewoon handig bij proeven en schoolexamens... #iknoemmaarswat


bron
- eh... dat is een docententaak en leg het een 't ander uit misschien?:-)
Of... zet het op je website...:-) wiskundeleraar.nl/page3ict.asp?n… #wiskundeB #HAVO - kan nog net....:-)
Of nog mooier expliciteer alles wat leerlingen moeten kennen, kunnen en begrijpen... #begripeninzicht zie bijvoorbeeld wiskundeleraar.nl/paGe3ict.asp?n…
Zie ook wiskundeleraar.nl/paGe3ict.asp?n… voor HAVO wiskunde A
...ook buitengewoon handig bij proeven en schoolexamens... #iknoemmaarswat


woensdag 16 mei 2018
Wiskundeleraar met beveiligde verbinding

- Veilige hosting via https
- 1 SSL certificaat
- 4 weken back-up plan
- 10 GB webruimte
- 5 GB e-mailruimte
- 20 GB dataverkeer
- 1 FTP-gebruiker
- 1 MySQL-database
- 1 mailinglijst
- DNS-beheer
dinsdag 8 mei 2018
donderdag 3 mei 2018
Week 30
In een kamer zijn acht lampen die onafhankelijk van elkaar aan en uit kunnen worden geschakeld.
- Hoeveel verschillende mogelijkheden zijn er om minstens vijf lampen aan te doen?
Week 29
25 leerlingen gaan met drie busjes naar een excursie. In het eerste en tweede busje kunnen negen leerlingen, in het derde kunnen zeven leerlingen mee.
- Op hoeveel manieren kun je de leerlingen in groepen van negen, negen en zeven verdelen?
woensdag 2 mei 2018
Week 28
Bij een familiefeest op nieuwjaarsdag zijn er vijf koppels aanwezig.
- Hoeveel mogelijkheden zijn er indien elke vrouw naast haar man wil zitten aan een ronde tafel ?
Week 27
Er zijn 9 mensen die een rondetafel-conferentie houden.
- Op hoeveel verschillende manieren kunnen zij zich om de ronde tafel schikken? Twee schikkingen waarbij iedere persoon dezelfde buren heeft worden niet als verschillend gezien.
dinsdag 1 mei 2018
Week 26
In een bepaalde stad zijn er twee taxibedrijven. Het ene heeft groene
taxi's, het andere blauwe. 75% van de taxi's zijn blauw, de overige 25%
zijn groen.
Op een nacht raakt een taxi betrokken in een ongeluk en pleegt vluchtmisdrijf. Er was een getuige die beweert dat de taxi groen was. Het gerecht onderzoekt het zicht van de getuige, gezien de duisternis op het ogenblik van het ongeluk.
Ze stellen vast dat de getuige in 80% van de gevallen de juiste kleur ziet, maar zich in 20% van de gevallen vergist.
Op een nacht raakt een taxi betrokken in een ongeluk en pleegt vluchtmisdrijf. Er was een getuige die beweert dat de taxi groen was. Het gerecht onderzoekt het zicht van de getuige, gezien de duisternis op het ogenblik van het ongeluk.
Ze stellen vast dat de getuige in 80% van de gevallen de juiste kleur ziet, maar zich in 20% van de gevallen vergist.
- Wat is de kans dat de taxi die in het ongeluk betrokken was inderdaad groen was, gegeven het feit dat de getuige 'groen' zei?
donderdag 26 april 2018
Publicatie: Wie zijn de leraren van morgen?
"Als obstakels worden genoemd: de hoge werkdruk, veel extra en onbetaalde werkzaamheden, lastige ouders, een slecht salaris en de tijd en moeite die het
kost om een lesbevoegdheid te halen."
vrijdag 20 april 2018
Week 25
Gegeven de balk \(ABCD.EFGH\) met \(AB=2\), \(BC=2\) en \(AE=4\). \(P\) ligt op het midden van \(AB\), \(Q\) ligt op het midden van \(BC\) en \(R\) ligt op het midden van \(GH\).
- Bereken de oppervlakte van \(\Delta PQR\)
Abonneren op:
Reacties (Atom)