Elektriciteitsverbruik

Ik had op elektriciteitsverbruik in eerste instantie gebruik gemaakt van integralen. Dat was vooral vanwege de oorspronkelijke titel 'integralen' en de gekozen categorie 'integreren'. Maar, zoals @GHvD opmerkte, zat er wel een addertje onder het gras. Met het verbruik per jaar zou je moeten rekenen met discrete waarden.

Daar zit wat in. Uiteindelijk ben ik er wel uitgekomen, geloof ik, maar wat nu precies de bedoeling was zullen we nooit weten...

Formule

$\eqalign{   & V_{gemiddeld}  = \frac{{S_{20} }} {{20}} = \frac{{3\root {10} \of 2  \cdot v_0 }} {{20(\root {10} \of 2  - 1)}} \cr}$

Voorbeeld

Neem $v_0=1000$. In Excel krijg je dan zoiets als:

jaar	verbruik
1	1.072
2	1.149
3	1.231
4	1.320
5	1.414
6	1.516
7	1.625
8	1.741
9	1.866
10	2.000
11	2.144
12	2.297
13	2.462
14	2.639
15	2.828
16	3.031
17	3.249
18	3.482
19	3.732
20	4.000
gemiddeld	2.240

De formule hierboven geeft $V_{gemiddeld}=2.239,9$ dus dat klopt...:-)


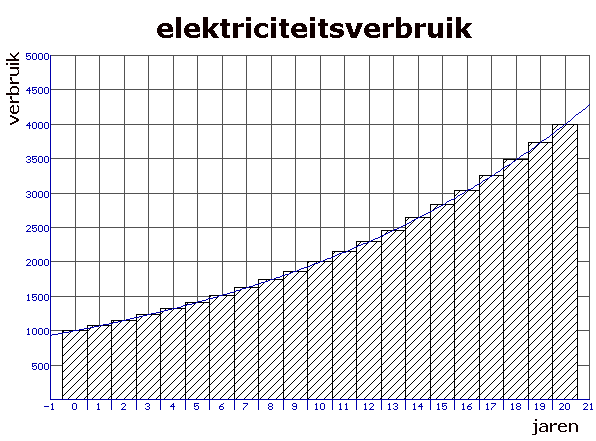
Hier kan je dan misschien toch nog wel iets doen met een integraal. Je moet wel even goed naar de grenzen kijken, maar dan heb je ook wat.

$\eqalign{V_{gemiddeld}  = \frac{{\int\limits_{t = \frac{1} {2}}^{20\frac{1} {2}} {1000 \cdot e^{\frac{{\ln (2)}} {{10}}t} dt} }} {{20}} \approx 2240,4}$

Of, maar dan meer in het algemeen, voor een willekeurige waarde van $v_0$:

$\eqalign{V_{gemiddeld}  = v_0  \cdot \frac{{3 \cdot \root {20} \of 2 }} {{2 \cdot \ln (2)}}}$

Ik bedoel maar. Ik vermaak me wel...:-)

• meetkundige rijen

Eindejaarsevaluatie 2018-2019

Precies:-)

One of the symptoms of an approaching nervous breakdown is the belief that one's work is terribly important.
Bertrand Russell

Wat moet je er mee?

De formule $a(n)=(n-1)(4n-3)$ geeft $a(23)=1958$.

• Wat moet je er mee?:-)

Ik ben er klaar mee...:-)

"After all is said and done, a lot more will be said than done."
Unknown
quotationspage.com/quotes/Unknown  
#mijnHML