KUBUSJES

Van n3 witte kubusjes bouw je een grote kubus van n bij n bij n.
De buitenkant van deze grote kubus kleur je rood. De kubus wordt weer afgebroken...
Er zijn nu verschillende kubusjes. Witte kubusjes, kubusjes met 1 rood vlak, kubusjes met 2 rode vlakken en er zijn zelfs kubusjes met 3 rode vlakken.
Hoeveel kubusjes zijn er van elk soort uitgedrukt in n?
Je zou denken dat dit toch niet al te moeilijk moet zijn, maar de resultaten vallen meestal tegen. Zou dat bedoeld worden met symbol sense? Of het ontbreken er van dan? Zoiets als ‘we hebben geen idee waar we mee bezig zijn….’.
Uitwerking
Als leerlingen dit lastig vinden geef ik als hint de suggestie om de verschillende aantallen ‘s uit te rekenen voor een kubus met n=10. Als je dan kan dan kan je ‘t mogelijkerwijs ook voor een willekeurige waarde van n.
Kubusjes met 3 rode vlakjes
Deze kubusjes zitten op de hoekpunten. Een kubus heeft 8 hoekpunten. Er zijn dus 8 kubusjes met 3 rode vlakjes.
Kubusjes met 2 rode vlakjes
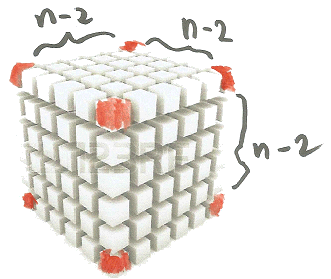
Deze kubusjes zitten op de ribben. Bij een ribbe van n kan je n-2
kubusjes vinden met twee rode vlakjes. Je hebt 12 ribben dus er zijn
12(n-2) kubusjes met twee rode vlakjes.
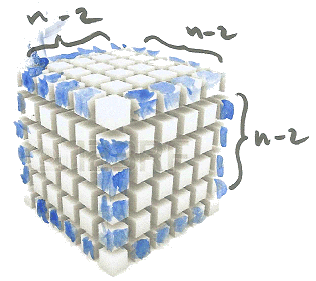
Kubusjes met 1 rood vlakje
Deze kubusjes zitten op de grensvlakken. Elk zijvlak bestaan uit (n-2)2 kubusjes met 1 rood vlakje. Er zijn 6 grensvlakken. Je hebt 6(n-2)2 kubusjes met 1 rood vlakjes.
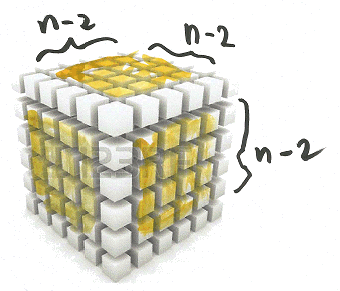
Kubusjes zonder rode vlakjes
De kubusjes die niet aan de buitenkant zitten hebben geen rode vlakjes.
Dat zijn er (n-2)3
Controle
Als het goed is moet 8 + 12(n-2) + 6(n-2)2 + (n-2)3 gelijk zijn aan n3. Dat klopt...
Daarmee is het probleem opgelost. Dat lijkt me toch niet zo heel erg moeilijk. Kennelijk zijn leerlingen dat niet gewend. Maar het kunnen ‘spelen met variabelen’ zou toch wel een handige vaardigheid kunnen zijn voor wiskunde B. Formules maken, optimaliseren, vergelijkingen of stelsels opstellen en oplossen…
Werk aan de winkel!
