Resultaten

Een boom van Pythagoras

Planning en uitstelgedrag

Het valt mij op dat sinds we een digitale jaarplanner gebruiken in de 4e klas leerlingen niet meer werken met de jaarplanner. 't Komt regelmatig voor dat leerlingen geheel verrast zijn als er een proef is. Dat is heel merkwaardig. Vooral als dat in de jaarplanner staat. Zo'n proef ligt dus al van tevoren vast...

Daarnaast gebruik ik op mijn website actueel waar ik laat zien wat we elke week doen. Meestal begin ik daar de les mee. Op dezelfde plek kunnen leerlingen zelfs met hun smartphone de agenda vinden. Dat is, zeg maar, de jaarplanner ONLINE.

Kortom: ergens klopt er iets niet.

Ik geloof dat leerlingen in HAVO 4 in 't algemeen zo'n 3 dagen voor een proef 's gaan kijken wat ze moeten doen. Vaak leidt dat tot een soort paniekreactie. O help... ik ben nog niet eens begonnen en nu al een proef. Als docent kan ik daar weinig mee. We zijn al 3 weken bezig met een hoofdstuk, je stelt de proef uit tot na de kerstvakantie en twee dagen voor de proef komt er een met de mededeling dat hij eindelijk z'n boek heeft teruggevonden maar dat het niet mogelijk is om een hoofdstuk in 2 dagen te doen en of ik misschien de proef kan uitstellen... zoiets...:-)

Hoe kan dat? Hoe moelijk is het om je aan de planning te houden? Een eerste stap zou al kunnen zijn om in ieder geval een planner te hebben. In het begin van het jaar heb ik daarvoor in 4e klas jaarplanners uitgedeeld. Maar die documenten zijn waarschijnlijk gebruikt om de open haard mee aan te maken...

• Jaarplanner HAVO 4 wiskunde A op 2 paginas
• Jaarplanner op één A4-tje

Ach ja... aan mij kan het niet liggen.

Drompel

Dit object bestaat uit een kegel, cilinder en een halve bol.

• Bereken de inhoud.

bron

Uit: de proefwerkbundel bij Netwerk

Somregel

In een vaas zitten 10 knikkers. 5 blauw, 3 rood en 2 wit. We halen steeds, met terugleggen 3 knikkers uit de vaas.

• Bereken de kans op 3 knikkers van dezelfde kleur

Uitwerking:

\(P(3\,blauwe\,knikkers)=\frac{5\cdot5\cdot5}{10\cdot10\cdot10}=0,125\)
\(P(3\,rode\,knikkers)=\frac{3\cdot3\cdot3}{10\cdot10\cdot10}=0,027\)
\(P(3\,witte\,knikkers)=\frac{2\cdot2\cdot2}{10\cdot10\cdot10}=0,008\)
\(P(3\,knikkers\,van\,dezelfde\,kleur)=0,125+0,027+0,008=0,160\)

Een mooi voorbeeld van de 'somregel'.

Extra oefening:

• Beantwoord dezelfde vraag, maar dan zonder terugleggen.

Zie kansbomen

Voorkennis hoofdstuk 4

Gemaakt voor HAVO 4 wiskunde B voorkennis hoofdstuk 4, maar ook bruikbaar in klas 3 bij hoofdstuk 6 (HAVO) c.q. hoofdstuk 7 (VWO).
START
Zie Voorkennis hoofdstuk 4 (B)

Navigatie website aangepast

Ik heb de navigatie van de website enigszins aangepast:

• http://www.wiskundeleraar.nl
• klas 2c
• klas 3b
• HAVO 4 wiskunde A
• HAVO 4 wiskunde B

Ook maar weer gedaan...:-)

Pi

14 15 92 65 35
89 79 32 38 46
26 43 38 32 79
50 28 84 19 71
69 39 93 75 10

Twee miljard honderdzevenenveertig miljoen vierhonderddrieëntachtigduizend zeshonderdzevenenveertig

\( \LARGE M_8 = 2^{31} - 1 = 2.147.483.647 \)

http://en.wikipedia.org/wiki/2147483647

Weekpuzzel 5

Je ziet hieronder een magisch vierkant:

• Welk getal staat er in het vakje met het vraagteken?

oplossing

Een vierkant en een cirkel

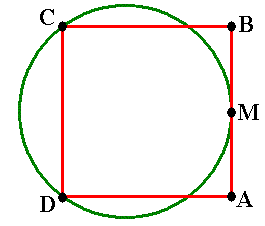
Het rode vierkant heeft een zijde van 50. Het punt M is het midden van AB en de groene cirkel gaat door de punten C, D en M.

Bereken exact de straal van deze cirkel.

---

• Een vierkant en een cirkel

Jan en Frans

Vergelijkingen in DWO

Naar aanleiding van 4. Hogeremachtsvergelijkingen heb ik een aantal dingen veranderd.

Bij opgave 9 stond zoiets als:



Dat kan natuurlijk wel, maar 'echt handig' is het niet. Het ging vooral om de rekenregels. De ABC-formule dat zal nu niet het probleem meer mogen zijn. Dan maar liever zoiets als:



Naar aanleiding van 5. Gebroken vergelijkingen zou je je nog kunnen afvragen waar die rekenregels eigenlijk goed voor zijn.



Dat kan zo wel (in dit geval) maar echt handig is het niet. Dit is volgens de rekenregels de juiste aanpak:



Er zijn ook gevallen waarbij je er niet aan ontkomt:



Ach ja... 't is zo leuk:-)

Resultaten procenteninstaptoets

De resultaten van de socrative procenteninstaptoets van vrijdag 7 februari 2014. Afgenomen in klas 3B:



Er is wel enige verwarring over het afronden. Als er niets bij staat dan rond je percentages af op 1 decimaal en geldbedragen op 2 decimalen. Ik moet nog even kijken of het helemaal overal duidelijk is. Maar de resultaten vallen mee. Niet alle leerlingen nemen het serieus, maar dat zegt dan ook weer iets.

Volgende week 'procenten en verhoudingstabellen'.

• Procenteninstaptoets | SOC-3070356 | socrative
• Instaptoets procenten | 10 vragen over procenten
• Procenten en verhoudingstabellen | met oefeningen

Zie ook Procenten

Weekpuzzel 4

• Hoeveel routes zijn er om in drie stappen van C naar A te gaan? Oplossing

Verschillende soorten procentsommen

Er zijn verschillende soorten opgaven met procenten. Schematisch krijg je dan zoiets als:

100%	12%	112%
€50	€6	€56

Je kunt dan allerlei verschillende sommen bedenken.

Voorbeeld 1
Dit jaar moet ik voor mijn abonnement op de krant 5% meer betalen dan vorig jaar, dat is wel €12 meer.

• Hoeveel moet ik dit jaar betalen voor de krant?

Oplossing

100%	5%	105%
...	€12	?

Kruislings vermenigvuldigen leert dan dat ik dit jaar voor het abonnement op de krant €252,- moet betalen.

Voorbeeld 2
Ik koop een CD-speler voor €142. Dat is dan inclusief 21% BTW.

• Hoeveel BTW betaal ik dan?

Oplossing

 

100%	21%	121%
...	?	€142

Je betaald dan €24,64 BTW.

Voorbeeld 3
In 2009 betaalde ik voor een retour naar Rotterdam €6,30. In 2010 betaal ik €7,20.

• Met hoeveel procent is de prijs van het retour toegenomen?

Oplossing

100%	?	...
€6,30	€0,90	€7,20

De prijs van een retour is toegenomen met 14,3%.

Conclusie?
Is dat handig? Is het nuttig? Werkbaar? Voorstelbaar? Verantwoord? Onthoudbaar? Structureerbaar? U zegt het maar...:-)

Hoe los je een vergelijking op?

Eh... bijvoorbeeld zo:

\(
\Large\begin{array}{l}
 1\frac{2}{3}x - 4 = 7 \\
 1\frac{2}{3}x = 11 \\
 5x = 33 \\
 x = 6\frac{3}{5} \\
 \end{array}
\)
Delen door een breuk is vragen om moeilijkheden...:-)

• Lineaire vergelijkingen met een breuk oplossen

De eerste 20 decimalen van pi

Driehoekskwadraatgetal

\( \Large N_k = \left( {\frac{{\left( {3 + 2\sqrt 2 } \right)^k - \left( {3 + 2\sqrt 2 } \right)^k }}{{4\sqrt 2 }}} \right)^2 \)

Square Triangular Number

Top

Ik heb in DWO een opdracht klaar gezet. Het mapje heet Ruimtelijke kijken en in dat mapje kan je twee opdrachten vinden:

1. Nabouwen met drie aanzichten
2. Nabouwen met twee aanzichten

Log in op DWO en maak alle opdrachten. Dat telt dan als proef voor hoofdstuk 5.

Zorg dat alle bolletjes groen zijn...



Niet allemaal groen, maar 192 punten in 88 minuten dat is toch mooi.\

• Ruimtelijk kijken