De afgeleide van een wortelfunctie

Naar aanleiding van afgeleide functie berekenen met wortel erin stond er op oefeningen 2 een oefening voor de afgeleide van een functie met een wortel. 't Is handig om dat met machten met gebroken exponenten te doen. Maar kan 't ook zonder?

Bereken de afgeleide van: \[ f(x) = \frac{4}{{\sqrt {2x^3 + 5x^2 + 4} }} \] Met de kettingregel en de standaardafgeleide van de wortelfunctie: \[ \begin{array}{l} f'(x) = - \frac{4}{{\left( {\sqrt {2x^3 + 5x^2 + 4} } \right)^2 }} \cdot \frac{1}{{2\sqrt {2x^3 + 5x^2 + 4} }} \cdot \left( {6x^2 + 10x} \right) \\ f'(x) = - \frac{{12x^2 + 20x}}{{\sqrt {\left( {2x^3 + 5x^2 + 4} \right)^3 } }} \\ \end{array} \] Met de quotiëntregel: \[ \begin{array}{l} f'(x) = \frac{{0 \cdot \sqrt {2x^3 + 5x^2 + 4} - 4 \cdot \frac{1}{{2\sqrt {2x^3 + 5x^2 + 4} }} \cdot \left( {6x^2 + 10x} \right)}}{{\left( {\sqrt {2x^3 + 5x^2 + 4} } \right)^2 }} \\ f'(x) = \frac{{ - 4 \cdot \frac{1}{{2\sqrt {2x^3 + 5x^2 + 4} }} \cdot \left( {6x^2 + 10x} \right)}}{{\left( {\sqrt {2x^3 + 5x^2 + 4} } \right)^2 }} \\ f'(x) = \frac{{ - 2\left( {6x^2 + 10x} \right)}}{{\left( {2x^3 + 5x^2 + 4} \right)\sqrt {2x^3 + 5x^2 + 4} }} \\ f'(x) = - \frac{{12x^2 + 20x}}{{\sqrt {\left( {2x^3 + 5x^2 + 4} \right)^3 } }} \\ \end{array} \] Kan ook...:-)

Mededelingen

VAKANTIE...

"Scholieren, studenten en docenten hebben vakantie wanneer hun school gesloten is en zij geen andere verplichtingen hebben."
bron

Kon nog net...

Nog even de jaarplanners van mavo 3, mavo 4, havo 4 wiskunde a en havo 5 wiskunde a in het atelier gezet... kon nog net voor 6 uur...

Laatste schoolweek

Agenda

Ik gebruik als agenda de GOOGLE-agenda, maar eigenlijk vind ik dat maar niks. In de werkruimte van havo 4 wiskunde B bijvoorbeeld heb ik al zoiets:



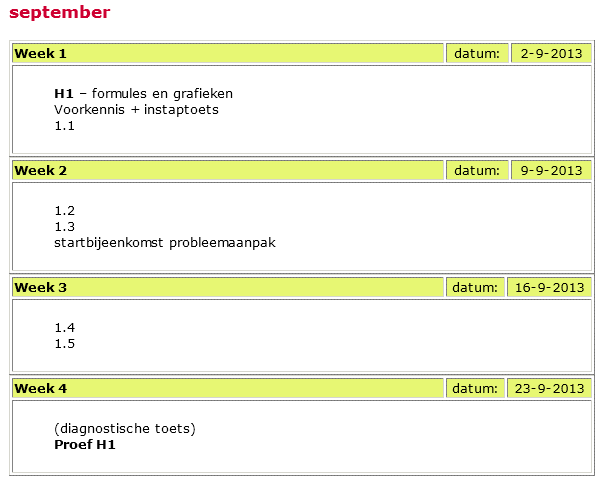
Dat lijkt me nogal duidelijk...

Teken een mogelijke grafiek

De opdracht 'teken een mogelijke grafiek' bij een aantal losse punten is altijd leuk. Als je zin hebt kan je echt uit je bol gaan... maar deze vond ik zelf nogal leuk.


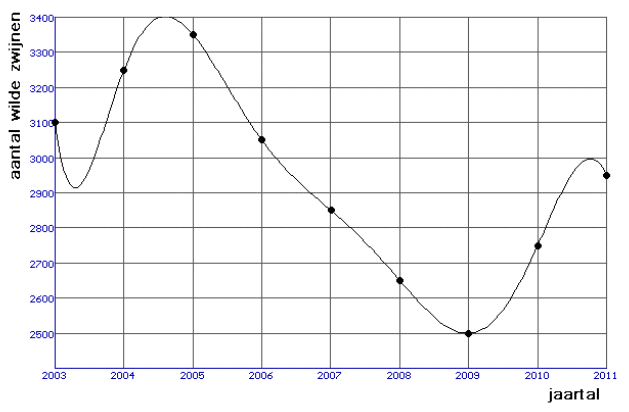
Hoe kom je er op? Tja... wie het weet mag het zeggen. Heb ik er zelf ook nog iets (van lol) aan...:-)