
woensdag 30 november 2016
dinsdag 29 november 2016
Goniometrische vergelijkingen
In hoofdstuk 8 van Getal & Ruimte van HAVO wiskunde B leren leerlingen o.a. om goniometrische vergelijkingen op te lossen. Zie goniometrische vergelijkingen voor een overzicht. Dat valt nog niet eens mee. Maar deze week heb ik toch weer 's iets ontdekt dat mogelijkerwijs kan helpen.
In het SE stond deze opgave:
Opgave 6
Het idee!?
Voor het berekenen van de hoek zet je je GR in. Dat ziet er dan (bijvoorbeeld) zo uit:
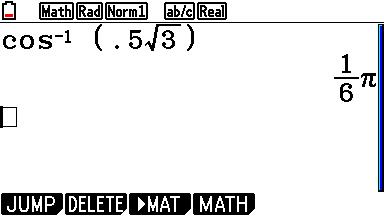
Je hebt dan al de helft van het antwoord te pakken! Met de eenheidscirkel en de cosinuslijn kan je dan de 'andere hoek' bepalen. Je bent dan al een stuk op weg. Mijn idee is dat dit beter werkt dan alles uit je hoofd doen.
In het SE stond deze opgave:
Opgave 6
Geef de exacte waarden van x met \(0 \leqslant x \leqslant 2\pi \)
- \(\cos (x) = \frac{1}{2}\sqrt 3\)
- \(\sin^2 (x + \frac{1}{3}\pi ) = 1\)
- \(\sin (\pi x) = \frac{1}{2}\sqrt 3\)
Het idee!?
Voor het berekenen van de hoek zet je je GR in. Dat ziet er dan (bijvoorbeeld) zo uit:

Je hebt dan al de helft van het antwoord te pakken! Met de eenheidscirkel en de cosinuslijn kan je dan de 'andere hoek' bepalen. Je bent dan al een stuk op weg. Mijn idee is dat dit beter werkt dan alles uit je hoofd doen.
maandag 28 november 2016
zondag 27 november 2016
Week 47
De rechthoekige driehoek raakt aan de cirkel.
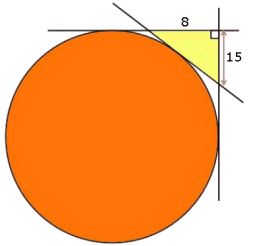

- Bereken exact de oppervlakte van de cirkel.
zondag 13 november 2016
vrijdag 11 november 2016
Week 45

Op hoeveel manieren kan men 8 kaarten trekken uit een spel van 52 kaarten als er precies 3 azen en 4 harten in moeten zitten?
donderdag 10 november 2016
vrijdag 4 november 2016
Dat kan ook...
Toon aan: \(\frac{1}{3} \cdot {}^2\log \left( {4x - 2} \right) = {}^8\log \left( {4x - 2} \right)\)
Een mini-opdracht
Wat zijn merkwaardige producten?
Volgens Wikipedia:
Veel gebruikte merkwaardige producten zijn:
\( \begin{array}{l} \left( {a + b} \right)^2 = a^2 + 2ab + b^2 \\ \left( {a - b} \right)^2 = a^2 - 2ab + b^2 \\ (a + b)(a - b) = a^2 - b^2 \\ \end{array} \)
Op de Wikipedia-pagina staan nog meer merkwaardige producten. Maar deze drie zijn al mooi genoeg...
Volgens Wikipedia:
De benaming merkwaardig product wordt in de algebra gebruikt om enkele
producten aan te duiden die het (be)merken waard zijn, dus waarvan het
goed is ze te onthouden.
Veel gebruikte merkwaardige producten zijn:
\( \begin{array}{l} \left( {a + b} \right)^2 = a^2 + 2ab + b^2 \\ \left( {a - b} \right)^2 = a^2 - 2ab + b^2 \\ (a + b)(a - b) = a^2 - b^2 \\ \end{array} \)
Op de Wikipedia-pagina staan nog meer merkwaardige producten. Maar deze drie zijn al mooi genoeg...
Jippie:-)
\(\begin{array}{l}
{\left( {1\frac{1}{2}} \right)^2} = {\left( {1 + \frac{1}{2}} \right)^2} = {1^2} + 2 \cdot 1 \cdot \frac{1}{2} + {\left( {\frac{1}{2}} \right)^2} = 1 + 1 + \frac{1}{4} = 2\frac{1}{4}\\
{\left( {2\frac{1}{2}} \right)^2} = {\left( {2 + \frac{1}{2}} \right)^2} = {2^2} + 2 \cdot 2 \cdot \frac{1}{2} + {\left( {\frac{1}{2}} \right)^2} = 4 + 2 + \frac{1}{4} = 6\frac{1}{4}\\
{\left( {3\frac{1}{2}} \right)^2} = {\left( {3 + \frac{1}{2}} \right)^2} = {3^2} + 2 \cdot 3 \cdot \frac{1}{2} + {\left( {\frac{1}{2}} \right)^2} = 9 + 3 + \frac{1}{4} = 12\frac{1}{4}\\
...\\
{\left( {n + \frac{1}{2}} \right)^2} = {n^2} + 2 \cdot n \cdot \frac{1}{2} + {\left( {\frac{1}{2}} \right)^2} = {n^2} + n + \frac{1}{4}
\end{array}\)
Abonneren op:
Posts (Atom)




