Tranformaties van grafieken

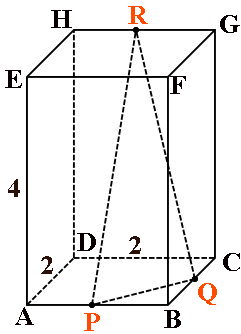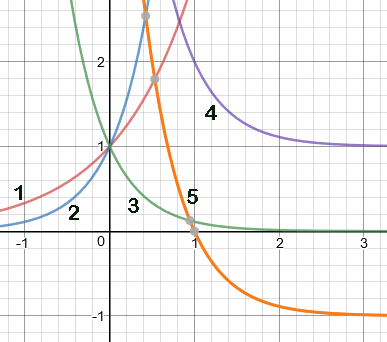
't Kwam vandaag nog even ter sprake.., transformaties van grafieken... waarbij iedereen mij altijd zo glazig zat aan te kijken... nu op papier...:-)

• 7. Transformaties van grafieken

Begeleidingsuren

Materiaal voor in de begeleidingsuren:

Welk deel is gekleurd?

Opgelost...:-)

SOLVE([2·s + 2·s + 2·s = 30, h + h + 2·s = 20, 2·f + 2·f + h = 13], [f, h, s])
[f = 2  h = 5  s = 5]
f := 2
h := 5
s := 5
s + h*f
15

Opgelost...:-)

Proof en pudding

\( \eqalign{ & \frac{{\cos \left( u \right) + \sin \left( u \right)}} {{\cos \left( u \right) - \sin \left( u \right)}} = \frac{{1 + \sin (2u)}} {{\cos (2u)}} \cr & \frac{{\left( {\cos \left( u \right) + \sin \left( u \right)} \right)\left( {\cos \left( u \right) - \sin \left( u \right)} \right)}} {{\left( {\cos \left( u \right) - \sin \left( u \right)} \right)^2 }} = \frac{{1 + \sin (2u)}} {{\cos (2u)}} \cr & \frac{{\cos ^2 \left( u \right) - \sin ^2 \left( u \right)}} {{\cos ^2 (u) - 2\sin (u)\cos (u) + \sin ^2 (u)}} = \frac{{1 + \sin (2u)}} {{\cos (2u)}} \cr & \frac{{\cos \left( {2u} \right)}} {{1 - \sin (2u)}} = \frac{{1 + \sin (2u)}} {{\cos (2u)}} \cr & \cos ^2 (2u) = 1 - \sin ^2 (2u) \cr & \sin ^2 (2u) + \cos ^2 (2u) = 1 \cr & {\text{Klopt!}} \cr} \)

Opgave

Programmeren voor dummies (2)

function kapIPv6(ip)
    dim s
    iF ip<>"" AND InStr(ip,":")>0 Then
        s=Replace(ip,":","|",1,3)
        s=Left(s,Instr(s,":")-1)
        s=Replace(s,"|",":",1,3)
        kapIPv6=s
    else
        kapIPv6=""
    end if
end function

Programmeren voor dummies

Function RemoveNumber(s)
     s=replace(s,"0. ","")
     s=replace(s,"1. ","")
     s=replace(s,"2. ","")
     s=replace(s,"3. ","")
     s=replace(s,"4. ","")
     s=replace(s,"5. ","")
     s=replace(s,"6. ","")
     s=replace(s,"7. ","")
     s=replace(s,"8. ","")
     s=replace(s,"9. ","")
     s=replace(s,"A. ","")
     s=replace(s,"B. ","")
     s=replace(s,"C. ","")
     s=replace(s,"D. ","")
     s=replace(s,"E. ","")
     s=replace(s,"F. ","")
     s=replace(s,"G. ","")
     s=replace(s,"H. ","")
     s=replace(s,"I. ","")
     s=replace(s,"J. ","")
     s=replace(s,"K. ","")
     s=replace(s,"L. ","")
     s=replace(s,"M. ","")
     s=replace(s,"N. ","")
     s=replace(s,"O. ","")
     s=replace(s,"P. ","")
     s=replace(s,"Q. ","")
     s=replace(s,"R. ","")
     s=replace(s,"S. ","")
     s=replace(s,"T. ","")
     s=replace(s,"U. ","")
     s=replace(s,"V. ","")
     s=replace(s,"W. ","")
     s=replace(s,"X. ","")
     s=replace(s,"Y. ","")
     s=replace(s,"Z. ","")
     RemoveNumber=s
End Function

Bezemklas

Bezemklas

In het kader van hulp voor wiskunde en het achterstallig onderhoud.

---

Opzet en werkwijze

---

• Voorbereiden op je SE.
• Extra uitleg en praktische tips.
• Vragen stellen.
• Samen opgaven en examenopgaven maken.
• Examentraining.
• Individuele bijles of in kleine groepjes (maximaal 4 leerlingen).
• Samenvattingen, uitwerkingen en checklists.
• Oefenen in de digitale wiskundeomgeving.
• Online ondersteuning.

---

Samenvatting en checklists voor SE1

---

• SE1 wiskunde A
• SE1 wiskunde B

---

Rooster voor hulp

---

• rooster

---

Handige hulpjes

---

• CASIO fx-CG 20

---

 

• bezemklas op wiskundeleraar.nl

Tips en truuks...

Puzzel

•  Welk deel van het vierkant is gekleurd?

Klas 3

Het was enigszins een verrassing maar we gebruiken in de derde klas dit jaar nog even Getal en Ruimte. De samenvattingen en checklists op wiskundeleraar kunnen dus nog een jaartje mee. Dat is dan wel weer aardig...:-)



Dat is dan gratis maar niet voor niets...:-)

HAVO wiskunde B

• formules, grafieken en vergelijkingen
• veranderingen
• hoeken en afstanden
• werken met formules
• machten, exponenten en logaritmen
• de afgeleide functie
• lijnen en cirkels
• goniometrie
• exponentiële verbanden
• meetkundige berekeningen
• verbanden en functies
• examentraining
  

HAVO wiskunde A

• rekenregels en verhoudingen
• verwerken van data
• tabellen en grafieken
• handig tellen
• lineaire verbanden
• statistiek en beslissingen
• statistiek met de computer
• veranderingen
• exponentiële verbanden
• statistische variabelen
• formules en vergelijkingen
• examentraining

WisFaq

Lerarentekort

Je ziet het gebeuren... Wij willen geen coach zijn wij zijn leraren... toch doen... wij willen geen groepen van 60-90... maar toch doen... Maar we willen ook geen #lerarentekort - in dat geval... maak een keus... zo niet... ga dan iets nuttigs doen... vuilnis ophalen of zo....:-)

Week 36

Deze week ben ik op school op therapeutisch basis begonnen. Ik ben maar 's niet naar school gegaan. De medische complicaties waren deze week nog een beetje te erg. Met fysio (2x), bedrijfarts en een behandeling in het WestEinde was de week ook wel weer goed gevuld. Volgende week een nieuwe kans...:-)

Voor school heb ik inmiddels NumWorks klaar gezet voor 4 en 5 HAVO wiskunde A en B. Dat was nog een werkje. Hoe deed ik dat ook alweer?  Maar dat is inmiddels wel gelukt. Volgens mij gaan we de instroommodules doen zoals ik die vorig jaar van plan was. Dat is mooi. Voor de rest van de dingen moeten we nog overleggen. Ik heb voor mijn collega's inmiddels ook de toetsen van 2016-2017 en 2017-2018 verzameld. Dat kan ze nog richting geven... en mogelijk een hoop werk besparen.

't Weekend staat voor de deur... dus vandaag doen we rustig aan.:-)

Numworks docenten

• Leerlingenversie (HTML5)
• Docentenversie met JAVA (Internet Explorer)
• Portable versie Docentomgeving zonder Java

Eindejaarsevaluatie 2017-2018

Nikolay Bogdanov-Belsky

In 1895, Nikolay Bogdanov-Belsky painted the famous: "Mental Arithmetic. In the Public School of S. Rachinsky." The problem on the blackboard is (10²+11²+12²+13²+14²)/365, can you find a way to solve it with mental arithmetic?

\( \eqalign{ & \frac{{10^2 + 11^2 + 12^2 + 13^2 + 14^2 }} {{365}} = \cr & \frac{{10^2 + \left( {10 + 1} \right)^2 + (10 + 2)^2 + (10 + 3)^2 + (10 + 4)^2 }} {{365}} = \cr & \frac{{5 \cdot 10^2 + 2 \cdot 10 + 4 \cdot 10 + 6 \cdot 10 + 8 \cdot 10 + 1 + 4 + 9 + 16}} {{365}} = \cr & \frac{{500 + 200 + 30}} {{365}} = \cr & \frac{{730}} {{365}} = 2 \cr} \)

Week 34

---

This is the end...

---

Met ingang van 18-7-2018 stop ik definitief met de weekpuzzels. 't Was leuk maar de koek is op...:-)

---

• Oplossing week 34

Week 32

ABCD is een vierkant met AE de deellijn van de hoek BAF.

• Bereken de lengte van AF.

---

• Oplossing week 32

Week 33

---

• Oplossing week 33

Week 31

Iemand heeft een rechthoekig stuk zink, 80 cm breed. Hij wil daarvan een goot maken met rechthoekige doorsnede.

• Ga na, wanneer de goot een zo groot mogelijke doorsnede heeft.

---

• Oplossing week 31

Calcudoku's

Getallen zijn mijn vrienden

• Examples for Numbers

Ook leuk:-)

Het berekenen van de snijpunten:

 \(
\eqalign{
  & \cos (x) = \cos (2x - 1)  \cr
  & x = 2x - 1 + k \cdot 2\pi  \vee x =  - (2x - 1) + k \cdot 2\pi   \cr
  &  - x =  - 1 + k \cdot 2\pi  \vee x =  - 2x + 1 + k \cdot 2\pi   \cr
  & x = 1 + k \cdot 2\pi  \vee 3x = 1 + k \cdot 2\pi   \cr
  & x = 1 + k \cdot 2\pi  \vee x = \frac{1}
{3} + k \cdot \frac{2}
{3}\pi  \cr}
\)

Dat zou zo maar kunnen...:-)

Grafieken en zo...

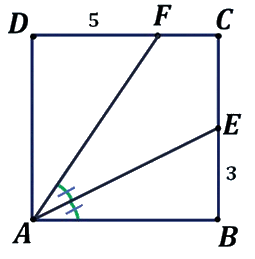
Maar wat is wat?

\( \eqalign{ & f(x) = (x - 2)^3 - 3 \cr & g(x) = f\left( {\frac{1} {2}x + 2} \right) \cr & h(x) = g(x) - f(x) \cr & i(x) = h'(x) \cr} \)

Om maar 's wat te noemen...:-)

In de driehoek van Pascal

In de driehoek van Pascal:

 \( \begin{array}{l} \left( {\begin{array}{*{20}c} n \\ k \\ \end{array}} \right) + 2 \cdot \left( {\begin{array}{*{20}c} n \\ {k - 1} \\ \end{array}} \right) + \left( {\begin{array}{*{20}c} n \\ {k - 2} \\ \end{array}} \right) = \\ \left( {\begin{array}{*{20}c} n \\ {k - 2} \\ \end{array}} \right) + \left( {\begin{array}{*{20}c} n \\ {k - 1} \\ \end{array}} \right) + \left( {\begin{array}{*{20}c} n \\ {k - 1} \\ \end{array}} \right) + \left( {\begin{array}{*{20}c} n \\ k \\ \end{array}} \right) = \\ \left( {\begin{array}{*{20}c} {n + 1} \\ {k - 1} \\ \end{array}} \right) + \left( {\begin{array}{*{20}c} {n + 1} \\ k \\ \end{array}} \right) = \\ \left( {\begin{array}{*{20}c} {n + 2} \\ k \\ \end{array}} \right) \\ \end{array} \)

---

• M. Bewijs

Gelijkzijdige driehoek

Trapformule

Magic Star Cube

WisFaq

Algebra	Analytische meetkunde	Anders
Bewijzen	Braille	Breuksplitsen
Complexegetallen	Cryptografie	Denkactiviteiten
Differentiaalvergelijking	Differentiëren	Docenten
Fibonacci en gulden snede	Formules	Fractals
Functies en grafieken	Geschiedenis	Getallen
Goniometrie	Grafen	Integreren
Kansrekenen	Kansverdelingen	Krommen
Limieten	Lineair programmeren	Lineaire algebra
Logaritmen	Logica	Numerieke wiskunde
Nummerborden	Oppervlakte en inhoud	Platonische lichamen
Praktische opdrachten	Prikbord	Puzzels
Rekenen	Rekenmachine	Rijen en reeksen
Ruimtemeetkunde	Software	Statistiek
Steekproeven	Telproblemen	Tovervierkanten
Vergelijkingen	Verzamelingen	Vlakkemeetkunde
Wiskunde en economie	Wiskunde en kunst	...

Aansluiting hoger onderwijs

Een aantal jaren geleden was er in het kader van aansluitproblemen toch wel een soort notie wat er zou moeten gebeuren. In het verslag van de bijeenkomst VO-HO aansluiting wiskunde 23 april 2007 kwam ik een 'wensenlijstje' tegen met ‘wat studenten wiskunde zouden moeten beheersen’:

• redeneren
• notaties kunnen lezen en schrijven
• gevoel voor abstractie
• een bepaalde werk- en studiehouding

Afbreken en dan weer opbouwen. Het blijft modderen met dat kind en het badwater. Nadruk op bepaalde vaardigheden leidt onherroepelijk tot een tekort op een ander gebied. Dat is niet handig, want zo schiet het natuurlijk op. Uiteindelijk blijft wel iedereen lekker bezig. Meer aandacht voor 'spelling' en 'rekenen' is leuk maar niet als dat dan weer ten koste gaat van iets anders.

Vroeger...:-)

De examensyllabi

"Volgens LAKS hadden leerlingen veel onduidelijkheid voor zichzelf kunnen voorkomen door de examensyllabi vooraf goed te lezen."
bron

---

- eh... dat is een docententaak en leg het een 't ander uit misschien?:-)
Of... zet het op je website...:-) wiskundeleraar.nl/page3ict.asp?n… #wiskundeB #HAVO - kan nog net....:-)
Of nog mooier expliciteer alles wat leerlingen moeten kennen, kunnen en begrijpen... #begripeninzicht zie bijvoorbeeld wiskundeleraar.nl/paGe3ict.asp?n…
Zie ook wiskundeleraar.nl/paGe3ict.asp?n… voor HAVO wiskunde A
...ook buitengewoon handig bij proeven en schoolexamens... #iknoemmaarswat

---

• https://twitter.com/wiswijzer

---

Wiskundeleraar met beveiligde verbinding

 

•     Veilige hosting via https
•     1 SSL certificaat
•     4 weken back-up plan
•     10 GB webruimte
•     5 GB e-mailruimte
•     20 GB dataverkeer
•     1 FTP-gebruiker
•     1 MySQL-database
•     1 mailinglijst
•     DNS-beheer 

Veilige hosting

Geogebra

---

• Zie Geogebra

---

• Zie ook Re: Brandpunt parabool

Week 30

In een kamer zijn acht lampen die onafhankelijk van elkaar aan en uit kunnen worden geschakeld.

• Hoeveel verschillende mogelijkheden zijn er om minstens vijf lampen aan te doen?

---

• Oplossing week 30

Week 29

25 leerlingen gaan met drie busjes naar een excursie. In het eerste en tweede busje kunnen negen leerlingen, in het derde kunnen zeven leerlingen mee.

• Op hoeveel manieren kun je de leerlingen in groepen van negen, negen en zeven verdelen?

---

• Oplossing week 29

Week 28

Bij een familiefeest op nieuwjaarsdag zijn er vijf koppels aanwezig.

• Hoeveel mogelijkheden zijn er indien elke vrouw naast haar man wil zitten aan een ronde tafel ?

---

• Oplossing week 28

Week 27

Er zijn 9 mensen die een rondetafel-conferentie houden.

• Op hoeveel verschillende manieren kunnen zij zich om de ronde tafel schikken? Twee schikkingen waarbij iedere persoon dezelfde buren heeft worden niet als verschillend gezien.

---

• Oplossing week 27

Week 26

In een bepaalde stad zijn er twee taxibedrijven. Het ene heeft groene taxi's, het andere blauwe. 75% van de taxi's zijn blauw, de overige 25% zijn groen.

Op een nacht raakt een taxi betrokken in een ongeluk en pleegt vluchtmisdrijf. Er was een getuige die beweert dat de taxi groen was. Het gerecht onderzoekt het zicht van de getuige, gezien de duisternis op het ogenblik van het ongeluk.

Ze stellen vast dat de getuige in 80% van de gevallen de juiste kleur ziet, maar zich in 20% van de gevallen vergist.

• Wat is de kans dat de taxi die in het ongeluk betrokken was inderdaad groen was, gegeven het feit dat de getuige 'groen' zei?

---

• Oplossing week 26

Publicatie: Wie zijn de leraren van morgen?

"Hieruit blijkt dat maar liefst veertig procent van de Nederlandse beroepsbevolking wel degelijk interesse heeft in werken in het onderwijs, maar dat hun beeldvorming erover een stuk negatiever is ten opzichte van mensen die al voor de klas staan."

"Als obstakels worden genoemd: de hoge werkdruk, veel extra en onbetaalde werkzaamheden, lastige ouders, een slecht salaris en de tijd en moeite die het
kost om een lesbevoegdheid te halen."

• bron

Wat zou volgens jou een goede manier zijn om meer mensen vanuit de beroepsbevolking het onderwijs in te krijgen?

Week 25

Gegeven de balk \(ABCD.EFGH\) met \(AB=2\), \(BC=2\) en \(AE=4\). \(P\) ligt op het midden van \(AB\), \(Q\) ligt op het midden van \(BC\) en \(R\) ligt op het midden van \(GH\).

• Bereken de oppervlakte van \(\Delta PQR\)

---

• Oplossing week 25