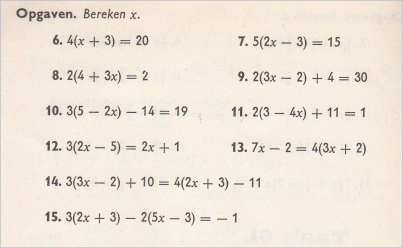Begrip en inzicht

Een opgave uit het SE voor HAVO 4 wiskunde B:

\(
\Large x(x^2 - 3)(x^3 + 2) = 0
\)

In 'het kader' van hogeremachtsvergelijkingen. Het is een soort geval van 'Als A·B=0 dan A=0 of B=0'. Je mag verwachten dat dit 'inzicht' inmiddels is doorgedrongen in HAVO 4.

In de herkansing stond deze opgave:

\(
\Large \left( {x^2 - 4} \right)\left( {x^2 - 2} \right) = 3
\)

Je hoeft geen helderziende te zijn om te voorspellen wat sommige leerlingen (bijvoorbeeld met een reproducerende leerhouding) dan gaan doen. Af en toe ben ik echt gemeen ergens, maar 't is voor een goede zaak...:-)

Waarmee ik maar wil zeggen dat je, naast kennis en vaardigheden, altijd moet proberen te begrijpen waar je mee bezig bent. Dat zou ik ook wel willen:-)

Kansrekenen

In vaas 1 zit 1 rode en 1 zwarte knikker. In vaas 2 zitten 2 rode en 3 zwarte knikkers. Je pakt uit elke vaas 1 knikker.

1. Bereken de kans op 2 rode knikkers.
2. Bereken de kans op 2 zwarte knikkers.
3. Bereken de kans op 1 rode en 1 zwarte knikker.

Je doet nu de knikkers van vaas 1 en vaas 2 in een nieuwe vaas. Je pakt uit deze nieuwe vaas 2 knikkers, zonder terugleggen.

1. Bereken de kans op 2 rode knikkers.
2. Bereken de kans op 2 zwarte knikkers.
3. Bereken de kans op 1 rode en 1 zwarte knikker.

Beantwoord dezelfde vragen voor de nieuwe vaas, maar nu met terugleggen.

1. Bereken de kans op 2 rode knikkers.
2. Bereken de kans op 2 zwarte knikkers.
3. Bereken de kans op 1 rode en 1 zwarte knikker.

...en dan heb je toch weer iets te doen...:-)

Grafische rekenmachine

• De grafische rekenmachine

Wiskunde: vaardigheden, begrip en inzicht

"The most important rule to master mathematics is: if you get lost (and most people including “experts” get lost a lot), back up to what you know and start over. Don’t try to keep going; in most cases, you will only get more lost."
bron

Zie ook:

• Wiswijzer
• WisFaq

Product-som-methode

Als je wilt dat de leerlingen in klas 2 een beetje begrijpen waar de product-som-methode vandaan komt dan zouden ze misschien eerst dit moeten doen:



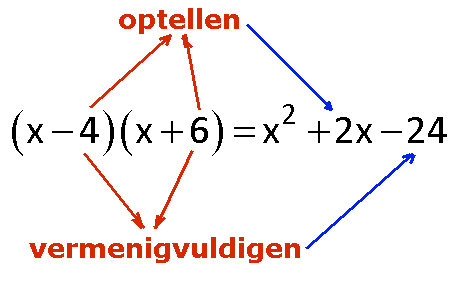
De product-som-methode is dan niets anders dan de weg terug... de andere kant op... van rechts naar links... geen haakjes wegwerken maar haakjes maken... wat was deze drieterm vroeger als product van twee tweetermen... enzo...

Opgelost

Er waren websitegewijs nog een paar dingen die voor verbetering vatbaar waren. Bij 't inloggen moet op de startpagina komen en niet op de pagina waar je 't laatst was. Als beheerder is dat wel handig, maar als docent of leerling is dat niet handig.

Als je inlogt met een verkeerde gebruikersnaam of wachtwoord zou het wel handig zijn om daarvan een melding te krijgen. Ook een goed idee...

Wel aan... dat is inmiddels opgelost. De navigatie verbetert en je krijgt nu een melding als je verkeerd inlogt:



Is dat leuk? Ja dat is leuk...:-)

Bereken 'x'

Zoiets als dit zou zo maar kunnen in de tweede klas:

• bron

Afronden 2

Bij afronden had ik deze opgave bij de opdrachten staan:



Ik geloof niet dat er iemand dat goed had. 't Is ook wel een beetje gemeen, maar we gaan school om iets te leren dus waarom niet?:-)



Zelf bedacht, heel ongeschikt voor een rekentoets, maar wel leuk genoeg om 's over te hebben.:-)

Afronden

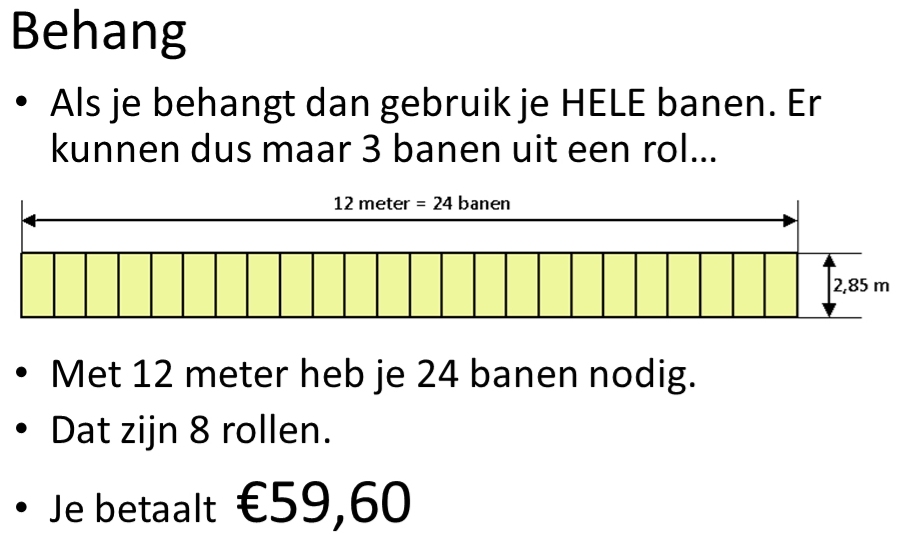
In klas 3 was er bij de proef van hoofdstuk 5/4 enige verwarring over afronden. Zoiets zat trouwens ook in de rekentoets:



Je kunt berekenen dat deze partij tegels €4096 kost. Je moet afronden op honderdtallen. Honderdtallen? Ja die... Je kijkt dan naar die '0' (dat zijn de honderdtallen) en besluit dat de tientallen 9 zijn dus afronden naar boven. Het antwoord is dan €4100. Je geeft antwoord in euro's, maar rondt wel af... op honderdtallen dus... een beetje vreemd?

Soortgelijke vragen in de toets:

1. Hoeveel mensen waren er werkzaam in de landbouw in 2007? Rond af op tienduizendtallen.
2. Hoeveel ha bestaat uit bossen en open natuurlijk terreinen? Rond af op duizendtallen.
3. Hoeveel filmpjes zijn dat per maand? Rond af op honderduizendtallen.
4. Hoeveel euro is dat per huishouden? Rond af op tientallen.
5. Hoeveel km zullen de in 2009 geproduceerde auto's in totaal afleggen? Rond af op miljarden.

Vraag 1
Hier geef je je antwoord in eenheden, maar je rondt wel af op tienduizendtallen. Dus 223.444 wordt dan 220.000. Een uitkomst als 4.666.666 zou dan 4.670.000 worden.

Vraag 2
Je geeft antwoord in ha. Een antwoord als 666.666 ha zou dan 667.000 ha worden. 12.345 ha wordt afgerond naar 12.000 ha.

Vraag 3
Als het antwoord 3.433.333 is dan wordt dat 3.400.000.

Vraag 4
Je geeft antwoord in euro's. Een antwoord als €8492 zou €8490 worden. Een uitkomst als €987 zou dan €990 worden.

Vraag 5
Je geeft je antwoord in kilometers. 34.555.444.999 km wordt dan afgerond naar 35.000.000.000 km. Normaal gesproken zou je dan (ook) 35 miljard km kunnen zeggen, maar formeel is het antwoord 35.000.000.000 km beter.

Kortom: kijk eerst in welke 'eenheid' je antwoord moet geven en rond dan af. Dat heeft niet noodzakelijkerwijs met decimalen te maken. Je kunt ook afronden op tientallen, tienduizentallen, miljoenen, .... Wat je maar wilt...:-)

't Is maar dat je 't weet:-)

Uitleg en oefenopgaven

Zonder herhaling...

Tien vragen kiezen uit een verzameling van meer dan 150 vragen, zonder herhaling? Dat is dan ook weer opgelost:

function KenOpgavenToe(UserID)
   dim vraagnummer, opgavenummer, error
   FOR vraagnummer=1 to 10
      opgavenummer=GeefOpgaveRandom(8376)
      WHILE StaatInDeLijst(UserID, opgavenummer)
         opgavenummer=GeefOpgaveRandom(8376)
      WEND 
      error=ZetOpdrachtInDatabase(UserID, vraagnummer, opgavenummer)
   NEXT
end function

't Is altijd belangrijk dat je zorgt dat het 'eindig' is, zullen we maar zeggen...:-)

De kapitein

Een voorbeeld van een probleem waar je mensen schrik mee kunt aanjagen is het kapiteinprobleem. De oplossing valt eigenlijk best mee. Zie wiswijzerblogspot voor een oplossing.

In WisFaq staan nog andere opmerkingen en oplossingen:

• Raadsel schip en kapitein
• Vergelijking oplossen d.m.v. een vraagstuk
  • Re: Vergelijking oplossen dmv een vraagstuk
• De kapitein

We noemen dit soort opgaven ook wel redactiesommen of verhaaltjessommen. Anderen spreken wel van context-opgaven. De contexten zijn meestal niet erg 'realistisch':-)

Een beetje lastig...?!

Uit de extra opgaven ruimtefiguren. Lichamen die passen in een kubus met ribben van 6 cm.

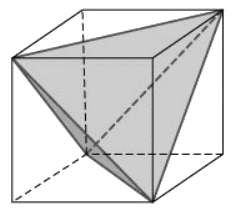
• Bereken de inhoud.

Je moet maar zien dat dit een kubus is met daaraf gesneden 4 piramides met een driehoek als grondvlak. Dat grondvlak is 18 cm² en de hoogte is 6. Dan kom je er wel uit, maar een beetje lastig is het wel...

Weekpuzzel 6

We hebben nu 5 weekpuzzels gehad.

• Wat is het antwoord van week 6?

...en dat was dan meteen de laatste weekpuzzel van dit jaar...

• oplossing