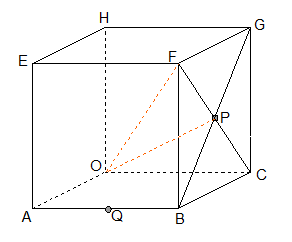
Teken een kubus EFGH ABCO met ribbe 3 cm. De x-as is de drager van OA, de y-as van OC en de z-as de drager van OH. P is het snijpunt van de zijvlaksdiagonalen BG en FC. Q is het midden van ribbe AB.
- Bereken de hoeken die lichaamsdiagonaal OF maakt met OP, OQ en OB.
- Bepaal een vectorvoorstelling van AG en BE. Bereken de hoek van OF en AG.
- Toon aan dat OF en BE elkaar loodrecht kruisen.
bron
De hoek bereken van OF en OP ging daarna goed. Maar bij de berekening van de hoek van OQ en OB kwam niet het goed antwoord. Er zaten in de uitwerkingen wel wat rekenfoutjes maar ook daarna wilde het niet lukken.
Ik moest er wel een tijd je naar kijken maar de hoek van OQ en OB wordt niet gevraagd. Je moet dat anders lezen:
Het gaat bij vraag a. om:
1. OF en OP
2. OF en OQ
3. OF en OB
...en niet om OQ en OB... Je moet er maar op komen.
Zo zie je maar weer dat ook bij wiskunde de taalvaardigheden erg belangrijk zijn. Wiskundig kan je dan nog zo slim zijn... als je slecht leest kom je nergens... ja in Rome misschien....:-)
....en vooruit: ik doe de uitwerking van a. er nog wel even bij...:-)
\( \begin{array}{l} \cos \varphi = \frac{{OF \cdot OP}}{{\left| {OF} \right| \cdot \left| {OP} \right|}} = \frac{{\left( {\begin{array}{*{20}c} 1 \\ 1 \\ 1 \\ \end{array}} \right) \cdot \left( {\begin{array}{*{20}c} 1 \\ 2 \\ 1 \\ \end{array}} \right)}}{{\left| {\left( {\begin{array}{*{20}c} 1 \\ 1 \\ 1 \\ \end{array}} \right)} \right| \cdot \left| {\left( {\begin{array}{*{20}c} 1 \\ 2 \\ 1 \\ \end{array}} \right)} \right|}} = \frac{4}{{\sqrt {18} }} \approx {\rm{0}}{\rm{,943}} \\ \varphi \approx 0,108\pi \\ \cos \varphi = \frac{{OF \cdot OQ}}{{\left| {OF} \right| \cdot \left| {OQ} \right|}} = \frac{{\left( {\begin{array}{*{20}c} 1 \\ 1 \\ 1 \\ \end{array}} \right) \cdot \left( {\begin{array}{*{20}c} 2 \\ 1 \\ 0 \\ \end{array}} \right)}}{{\left| {\left( {\begin{array}{*{20}c} 1 \\ 1 \\ 1 \\ \end{array}} \right)} \right| \cdot \left| {\left( {\begin{array}{*{20}c} 2 \\ 1 \\ 0 \\ \end{array}} \right)} \right|}} = \frac{3}{{\sqrt {15} }} \approx {\rm{0}}{\rm{,775}} \\ \varphi \approx 0,218\pi \\ \cos \varphi = \frac{{OF \cdot OB}}{{\left| {OF} \right| \cdot \left| {OB} \right|}} = \frac{{\left| {\left( {\begin{array}{*{20}c} 1 \\ 1 \\ 1 \\ \end{array}} \right)} \right| \cdot \left| {\left( {\begin{array}{*{20}c} 1 \\ 1 \\ 0 \\ \end{array}} \right)} \right|}}{{\left| {\left( {\begin{array}{*{20}c} 1 \\ 1 \\ 1 \\ \end{array}} \right)} \right| \cdot \left| {\left( {\begin{array}{*{20}c} 1 \\ 1 \\ 0 \\ \end{array}} \right)} \right|}} = \frac{2}{{\sqrt 6 }} \approx {\rm{0}}{\rm{,816}} \\ \varphi \approx 0,196\pi \\ \end{array} \)
Zo heb ik zelf moeite met het verschil tussen 'groter' en 'kleiner'. Dat is niet handig voor een wiskundeleraar. Idem voor 'links' en 'rechts'. Dat is dan weer lastig bij rijles en navigatie... Over Rome gesproken...:-)
