Vandaag ben ik 4 HAVO wiskunde B begonnen met probleemaanpak. De jaarlijkse praktische opdracht omtrent de aanpak van wiskundige problemen.PROBLEEMAANPAK
- Startbijeenkomst
- Wiskundige problemen om op te lossen
- Toets in tweetallen
De vlaggenmast
Een vlaggenmast is stevig in de grond bevestigd. Hij is 10 meter hoog en door een harde rukwind afgebroken. Het afgebroken stuk zit nog wel vast aan het stuk dat in de grond zit. De top van de mast is op 3 meter van de voet op de grond terecht gekomen.
- Op welke hoogte (vanaf de grond) is de mast afgebroken?
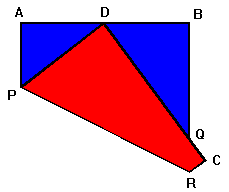
Hierboven zie je een vierkant blaadje ABCD van 8 bij 8 cm. Eén hoekpunt van het blaadje is op zo'n manier over het blaadje heen gevouwen dat D precies in het midden van AB ligt.
- Bereken EXACT de lengte van BQ en DQ.
De driedeling van de hoek
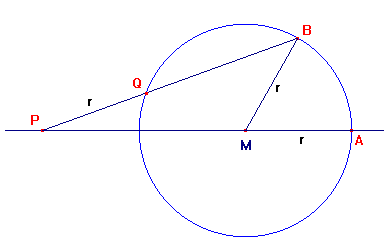
Gegeven is een cirkel met middelpunt M en straal r. Op de cirkel heb je de punten A en B. De lijn PB snijdt de cirkel in het punt Q en wel zo dat PQ=r.
- Toon aan dat \(\angle\)AMB drie keer zo groot is als \(\angle\)APB
Bij de uitwerkingen heb ik geprobeerd om expliciet te vermelden welke 'algemene principes' hierbij handig zijn om te onthouden en te gebruiken:
- Als je te maken hebt met een rechthoekige driehoek dan weet je dat de stelling van Pythagoras geldt. Daarmee kan je (ook met variabelen) relaties leggen tussen rechtshoekszijden en de schuine zijde.
- Als je een lengte van een lijnstuk niet kent, maar dat wel graag zou willen weten, probeer dan 's voor de lengte x te nemen en dan een andere zijde uit te drukken in x. Voer één of meer variabelen in.
- Als je 'ergens' twee driehoeken ziet van dezelfde vorm probeer dan eens iets te doen met gelijkvormigheid.
- Als je te maken hebt met cirkels is het altijd handig om even goed te kijken of je iets moet doen met het middelpunt van de cirkel. Je moet ook altijd even kijken naar de straal. Waar kan je die allemaal terug vinden?
- Let op bijzonder figuren zoals gelijkzijdige, gelijkbenige of rechthoekige driehoeken. Wat weet je allemaal van zo'n bijzonder figuur? Idem voor cirkels en vierhoeken.
- Als je een algemeen geval niet direct op kan lossen probeer het dan ' s met een concreet voorbeeld. Ik had even 20 genomen om te kijken of het dan wel lukt. Dat lukt. Maar als je iets kunt uitrekenen met getallen dan kan dat ook met een variabele. Maak dezelfde stappen en dan lukt dat...:-)
Alles bij elkaar een nuttige les, denk ik. Vrijdag deel 2.
