Maar dan tel je de zijden ook mee...
Het aantal diagonalen is \(
\left( {\begin{array}{*{20}c}
n \\
2 \\
\end{array}} \right) - n
\)
Dat kan ook:-)
Ik doe dat zelf meestal anders: uit elk hoekpunt vertrekken \(n-3\) diagonalen. Dat zijn in totaal dan \(n(n-3)\) vertrekkende diagonalen, maar dan tel je alles dubbel, dus het aantal diagonalen is gelijk aan \(\frac{1}{2}n(n-3)\).
Maar dat is gelukkig hetzelfde...:-)
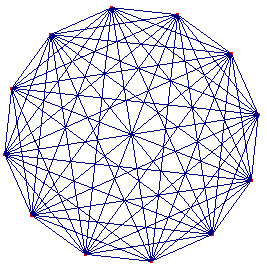
- hoeveel diagonalen heeft een n-hoek?
- een soort van toepassing maar dan anders...:-)
